Question

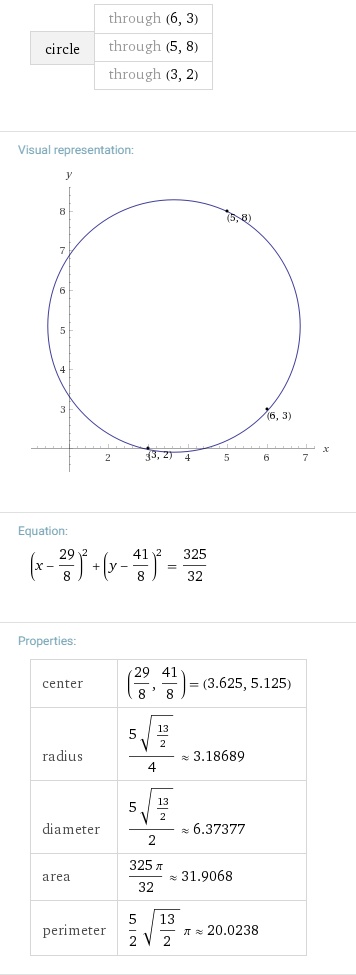
A triangle has vertices `(6 ,3 )`, `(5 ,8 )`, and `(3 ,2 )`. What is the area of the triangle's circumscribed circle?

Answer 1

`text{circumcircle area }= {325 pi}/32`

Explanation:

At first glance this has something to do with a triangle.

At second glance we see this is really just asking for the area of the circle through the three given points; it doesn't have much to do with the triangle per se.

At third glance we work out the math and conclude the squared radius of the circumcircle is the product of the squared lengths of the triangle divided by its sixteen times its squared area. So the triangle matters after all. I worked it out here; I won't repeat it. In symbols:

`r^2 = {a^2b^2 c^2}/{16 A^2}`

Here `a,b,c` are the sides and `A` the area of the triangle. `r` is the radius of the circumcircle.

It's tempting, but don't take the square root. It's much easier to work with in this form. Plus, we're after the area of the circumcircle, `\pi r^2`, so we just work at the squared level.

The squared lengths are easily gotten from the coordinates.

`a^2 = (6-5)^2+(3-8)^2=26`

`b^2 = (5-3)^2+(8-2)^2=40`

`c^2 = (6-3)^2+(3-2)^2 = 10`

There are a few ways to get the area of the triangle. We could use Heron, which would be really ugly, with lots of fractions and four square roots. We could use the Shoelace Theorem, which is usually the best choice to determine the area of polygon given planar coordinates. But we'll use Archimedes' Theorem, a modern form of Heron's Formula. It gives the squared area in terms of the square lengths, which we already calculated. In fact, it gives `16A^2` directly:

`16A^2 = 4a^2 b^2 - (c^2 - a^2 - b^2)^2`

`a,b` and `c` are of course interchangeable in the area formula.

`16A^2 = 4(26)(40) - (10-26-40)^2 = 1024`

Perfect square; we actually have a natural number for the area of the triangle. I know nobody cares but that's the kind of thing I notice.

OK, we're home.

`text{circumcircle area} = pi { (26)(40)(10)}/1024`

`text{circumcircle area }= {325 pi}/32`

Check: Alpha