A triangle has corners at #(6 ,3 )#, #(7 ,4 )#, and #(1 ,2 )#. How far is the triangle's centroid from the origin?

Question

1264 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-14T04:24:21

Distance of centroid from origin is

#OG = sqrt((14/3)^2 + 3^2) = color (blue)(5.5478)#

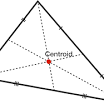
enter image source here

Centroid (g) is the concurrent point of the three medians of a triangle.

#g# is one third distance from the mid point of the base and two thirds from the corresponding vertex.

Hence centroid (g) coordinates are calculated using the formula

#G_x = (x_a + x_b + x_c) / 3, G_y = (y_1 + y_2 + y_3) / 3# where A, B, C are the three vertices of the triangle.

#G_x = (6+7+1)/3 = 14/3#

#G_y = (3+4+2) / 3 = 3#

Coordinates of centroid #G (14/3, 3)#

Coordinates of origin #O (0,0)#

Distance of centroid from origin is

#OG = sqrt((14/3)^2 + 3^2) = color (blue)(5.5478)#