A triangle has corners at #(6 ,8 )#, #(1 ,5 )#, and #(3 ,9 )#. What is the area of the triangle's circumscribed circle?
1 Answer
Feb 28, 2018
Follow the steps as listed out below to find the area of the circumcircle.
Explanation:
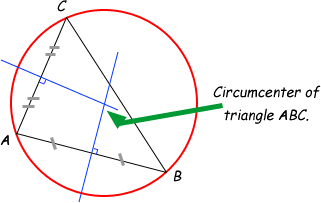
- Find and Calculate the midpoint of given coordinates or midpoints (AB, AC, BC)
- Calculate the slope of the particular line
- By using the midpoint and the slope, find out the equation of line (y-y1) = m (x-x1)
-
Find out the other line of equation in the similar manner
-
Solve the two bisector equation by finding out the intersection point
- Calculated intersection point will be the circumcenter of the given triangle
- Calculate the distance between circumcenter and one of the vertices to get the measure of radius.
- Find the area of the circumcircle using the circle area formula
#A = pi r@^2#