Question

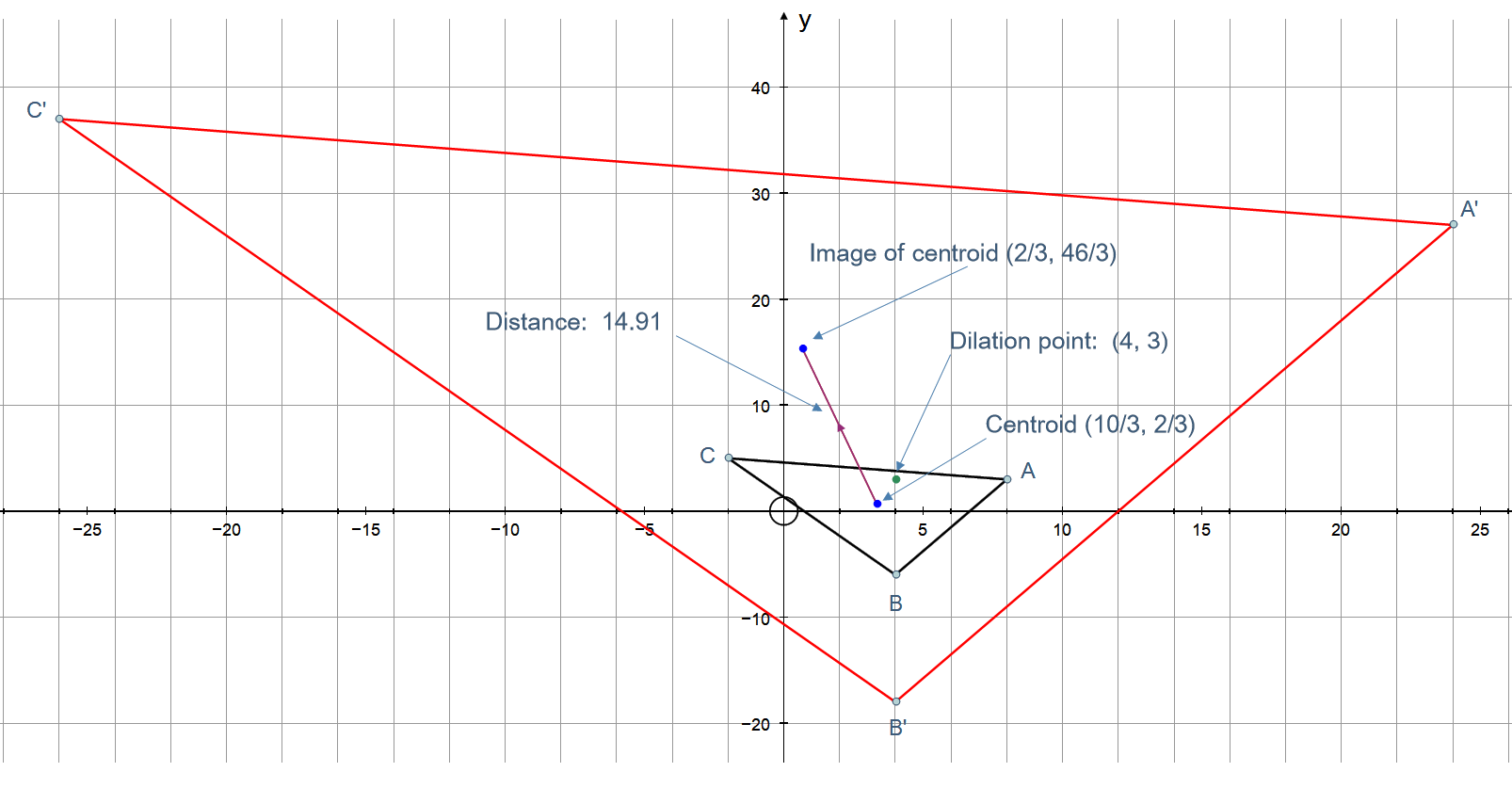
A triangle has corners at `(8 ,3 )`, `(4 ,-6 )`, and `(-2 ,5 )`. If the triangle is dilated by a factor of `5` about point #(4 ,-3 ), how far will its centroid move?

Answer 1

`color(blue)((20sqrt(5))/3 " units")`

Explanation:

When the vertices of the triangle are dilated by a factor of 5 about the point `(4,-3)`, the centroid will also be dilated by the same factor about the same point. This being the case, we only need to find the centroid of the original triangle and dilate this to find the centroid of the triangles image.

The centroid can be found by taking the arithmetic mean of the x coordinates and the y coordinates.

`((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)`

`"centroid"=((8+4-2)/3,(3-6+5)/3)=(10/3,2/3)`

We can dilate this using vectors:

Let `vec(OD)=((4),(-3))` be position vector of dilation point.

Let `vec(OC')` be the position vector of the centroids image.

Then:

`vec(DC)=((-2/3),(11/3))`

Then dilating by a factor of 5:

`vec(OC')=vec(OD)+5vec(DC)=((4),(-3))+5((-2/3),(11/3))=((2/3),(46/3))`

Distance the centroid has moved can be found using the distance formula:

`d=sqrt((10/3-2/3)^2+(2/3-46/3)^2)=(20sqrt(5))/3`

PLOT: