A triangle has corners at #(9 ,1 )#, #(6 ,7 )#, and #(3 ,2 )#. How far is the triangle's centroid from the origin?
1 Answer
The triangle's Centroid is
Explanation:
Construct a triangle ABC with Vertices as given:
A Centroid of a triangle ABC is the point where the three medians of the triangle meet.
A median of a triangle is a line segment from one vertex to the mid point on the opposite side of the triangle.
Mark the Mid-Points of the line segments
Call these mid-points
Mid-Point of Side
Mid-Point of Side
Mid-Point of Side
Join Side
Join Side
Join Side
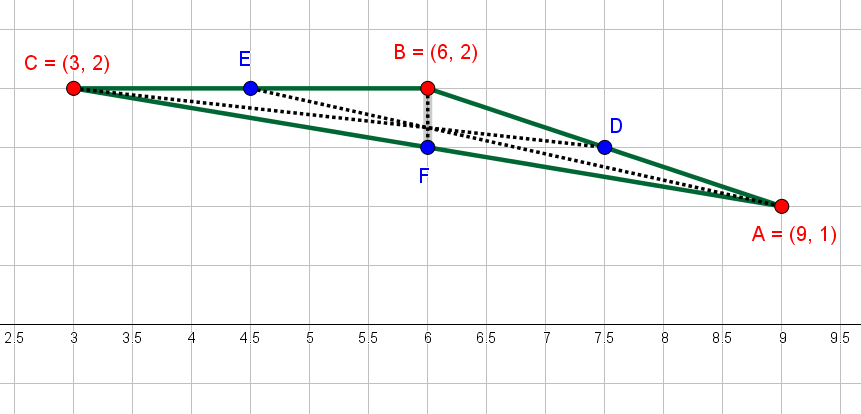
You can see that the all the three Medians intersect at a point.
This point is called the Centroid.
Identify the Origin (O) with coordinates
Mark the Centroid and name it as Centroid.
Connect the Origin and the Centroid.
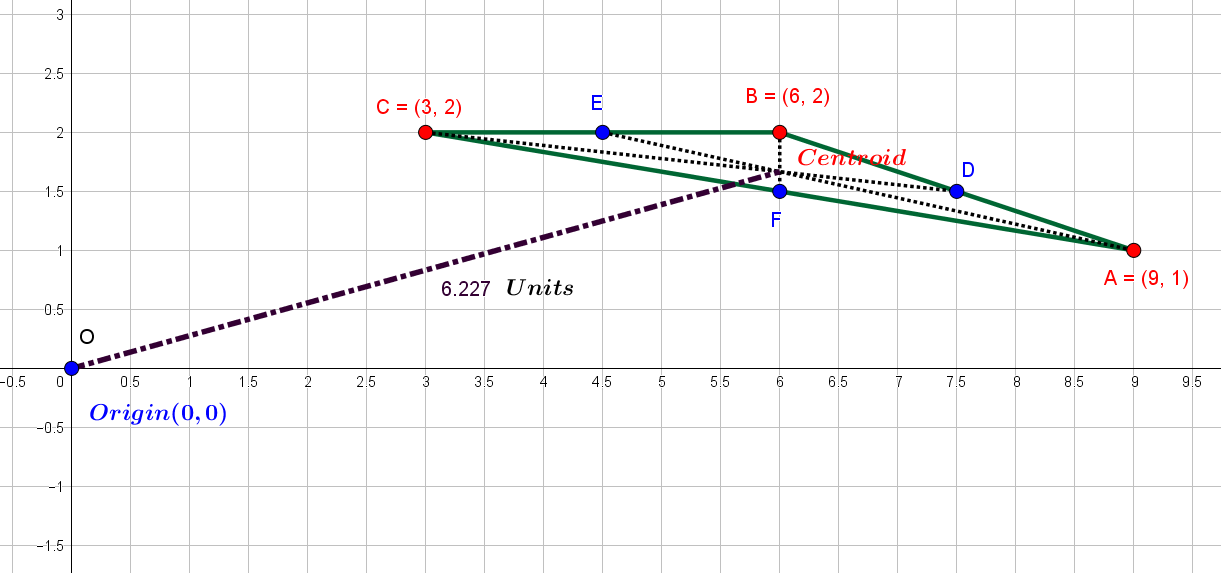
Measure the length of the line segment joining the Origin and the Centroid.
The magnitude
Hence, the required answer.
You can write your final solution as:
The triangle's Centroid is
An interesting observation to note:
The three line segments
This property is known as Ceva's Theorem.
Hope it helps.

