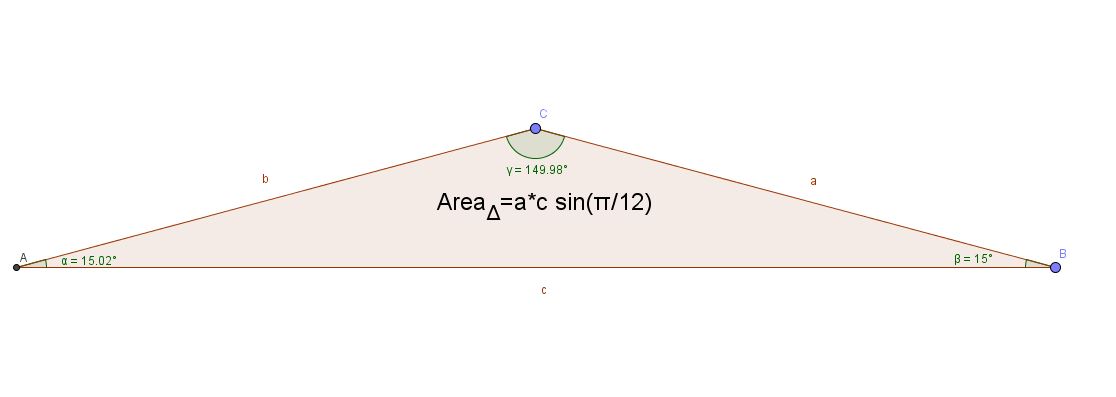
Firs by AA the triangle is isosceles triangle with sides #a=b# see geometric figure. Thus using the sine law and the cross product we can write:
1) #a/sinalpha = b/sinbeta = c/singamma#
2) #A_Delta =1/2 |a|*|c|*sin(alpha)= 1/2(ac)sin(alpha)#
3) #a=b " and " alpha = beta = pi/12 #
From 1) we have #a = sinalpha/singamma c#
Substitute into 2) #2A_Delta=sin^2alpha/sinbeta c^2#
Now letting #A_Delta=8; sinalpha=sin(pi/12); sinbeta= sin(5/6pi)#
#16=sin^2(pi/12)/sin(5/6pi) c^2#
#c=sqrt(16*sin(5/6pi)/sin^2(pi/12))=(4)/sin(pi/12)sqrt(sin(5/6pi))#
#c=(4*2)/sqrt((2-sqrt(3)))color(red)(sqrt(sin(5/6pi)) #
#color(red)(sqrt(sin(5/6pi)) = color(blue)(cos(pi/2-5/6pi)=cos(pi/3)=1/2)#
#c=(4*2)/sqrt((2-sqrt(3)))color(blue)(1/2)=(4)/sqrt(2-sqrt(3) )#
#a= sin(pi/12)/cos(pi/3)*(4)/sqrt(2-sqrt(3) ) = 4 =b#
Now the task is to find the radius of the Incenter, Inradius #r_Delta#
#r_Delta = A_Delta/P_Delta# Where
#A_Delta# = Area and #P_Delta# = Perimeter
#r_Delta = 8/(8+(4)/sqrt(2-sqrt(3))#
An the #A_(o.) = pi*r_Delta^2 =[8/(8+4/sqrt(2-sqrt(3)))]^2pi#
#A_(o.) ~~ [8/(8+7.73)]^2pi~~.259pi#