A triangle has vertices A, B, and C. Vertex A has an angle of #pi/12 #, vertex B has an angle of #pi/8 #, and the triangle's area is #9 #. What is the area of the triangle's incircle?

Question

1629 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-22T09:32:20

#color(indigo)("Area of incircle " = pi r^2 = pi * (0.8318)^2 = 2.174#

#hat A = pi/12, hat B pi/8, hat C = (19pi) / 24), A_t = 9#

#A_t = (1/2) ab sin C = (1/2(bc sin A = (1/2) ac sin B#

#ab =( 2A_t) /sin C = (2 * 9) / sin ((19pi)/24) = 29.57#

#bc = (2 * 9) / sin (pi/12) = 69.55#

#ca = (2 * 9) / sin (pi/8) = 47 04#

#a = sqrt(abc)^2 / (bc) =sqrt (29.57 * 69.55 * 47.04) / 69.55 = 4.48#

#b = sqrt(abc)^2 / (ac) =sqrt (29.57 * 69.55 * 47.04) / 47.04 = 6.62#

#c = sqrt(abc)^2 / (ab) =sqrt (29.57 * 69.55 * 47.04) / 29.57 = 10.54#

#"Semiperimeter " = s = (a = b + c) / 2 = (4.48 + 6.62 + 10.54) / 2 = 10.82#

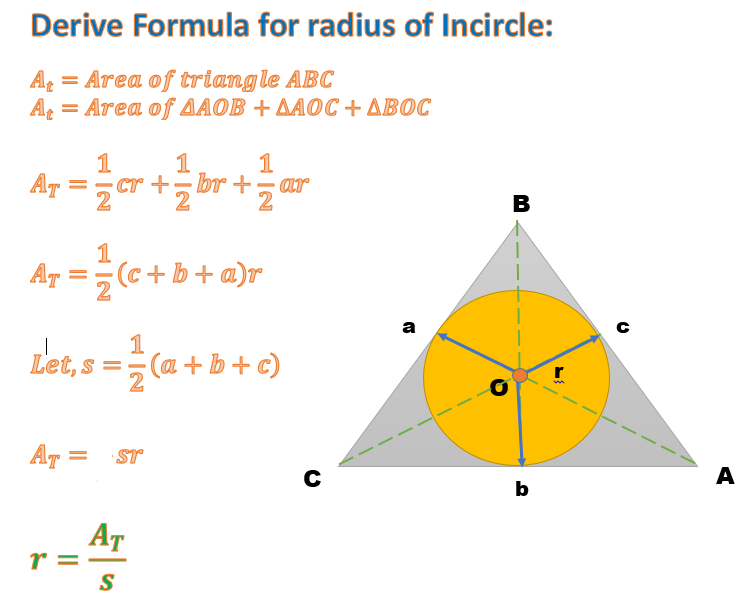
#color(chocolate)("Incircle radius " = r = A_t / s = 9 / 10.82 = 0.8318#

#color(indigo)("Area of incircle " = pi r^2 = pi * (0.8318)^2 = 2.174#