A triangle has vertices A, B, and C. Vertex A has an angle of #pi/12 #, vertex B has an angle of #(5pi)/8 #, and the triangle's area is #8 #. What is the area of the triangle's incircle?

Question

1270 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-19T06:55:35

#color(magenta)("Area of inscribed circle " = A_i = pi r^2 ~~ 2.442#

#"Area of "Delta = A_t = (1/2) a b sin C = (1/2) b c sin A = (1/2) c a sin B#

#"Given " hat A = pi/12, hat B = (5pi)/8, hat C = ((7pi)/24)#, A_t = 8#

#a b = (2 A_t) / sin C = 16 / sin ((7pi)/24) ~~ 20.1676#

#b c = (2 A_t) / sin A = 16 / sin (pi/12) = 61.8193#

#c a = (2 A_t) / sin B = 16 / sin ((5pi)/8) = 17.3183#

#a = (a b c) / (b c) = sqrt(20.1676 * 61.8193 * 17.3183) / 61.8193 = 2.3769#

#b = (a b c) / (c a) = sqrt(20.1676 * 61.8193 * 17.3183) / 17.3183 = 8.4847#

#c = (a b c) / (a b) = sqrt(2.3769 * 61.8193 * 17.3183) / 20.1676 = 7.286#

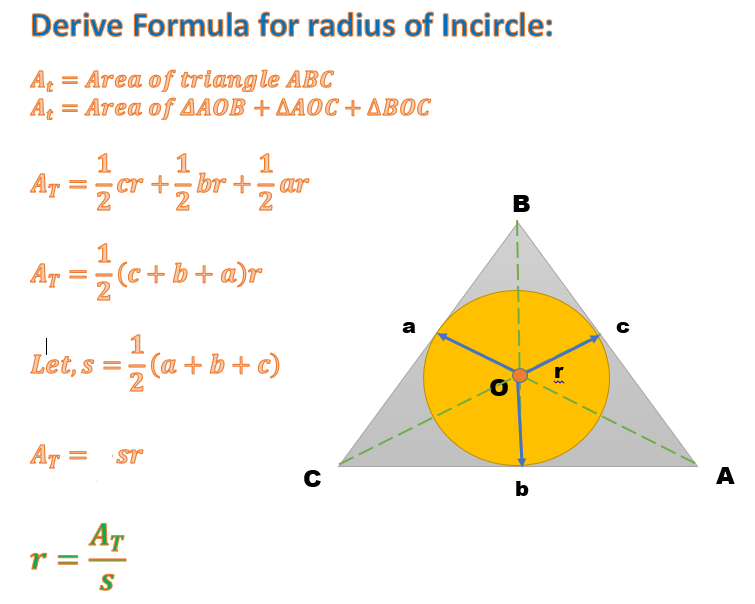
#"Semi-perimeter " = s = (a + b + c) / 2 = 18.1476 / 2 = 9.0738#

#"Radius of inscribed circle " = r = A_t / s = 8 / 9.0738#

#color(magenta)("Area of inscribed circle " = A_i = pi r^2 = pi * (8/9.0738)^2 ~~ 2.442#