A triangle has vertices A, B, and C. Vertex A has an angle of #pi/2 #, vertex B has an angle of #( pi)/4 #, and the triangle's area is #16 #. What is the area of the triangle's incircle?

Question

1320 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-27T02:30:42

#color(crimson)("Area of inscribed circle " = A_i = pi r^2 = 8.6186#

#"Area of "Delta = A_t = (1/2) a b sin C = (1/2) b c sin A = (1/2) c a sin B#

#"Given " hat A = pi/2, hat B = pi/4, hat C = pi/4, A_t = 16#

It's an isosceles right triangle.

#a b = (2 A_t) / sin C = 32 / sin (pi/4) = 45.25#

#b c = (2 A_t) / sin A = 32 / sin (pi/2) = 32#

#c a = (2 A_t) / sin B = 32 / sin (pi/4) = 45.25#

#a = (a b c) / (b c) = sqrt(45.25 * 45.25 * 32) / 32 = 8#

#b = (a b c) / (c a) = sqrt(45.25 * 45.25 * 32) / 45.25 = 5.66#

#c = (a b c) / (a b) = sqrt(45.25 * 45.25 * 32) / 45.25 = 5.66#

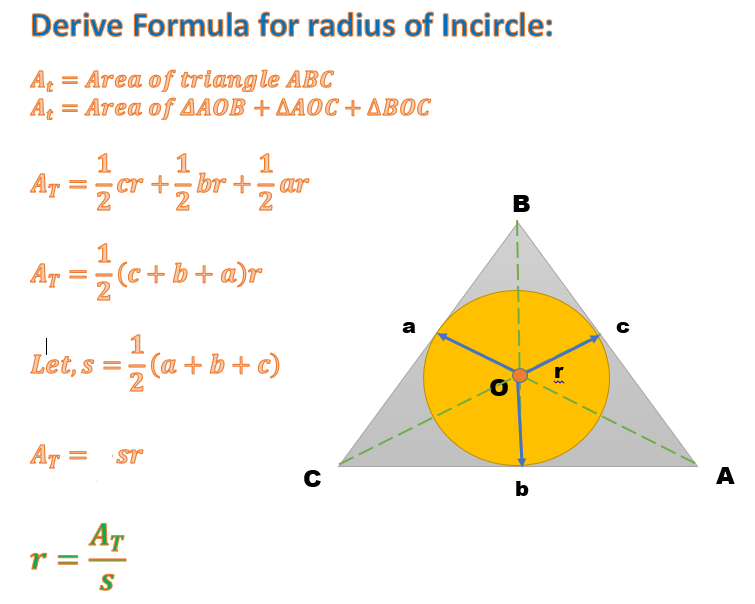
#"Semi-perimeter " = s = (a + b + c) / 2 = 19.32 / 2 = 9.66#

#"Radius of inscribed circle " = r = A_t / s = 16 / 9.66 = 1.66#

#"Area of inscribed circle " = A_i = pi r^2 = pi * 1.66^2 = 8.6186#