Question

A triangle has vertices A, B, and C. Vertex A has an angle of `pi/2`, vertex B has an angle of `( pi)/8`, and the triangle's area is `98`. What is the area of the triangle's incircle?

Answer 1

Area of Incircle `A_i = 40.72` sq units

Explanation:

`hatA = pi/2, hatB = pi/8, hat C = pi - pi/2 - pi/8 = (3pi)/8, A_t = 98`

Next we have to find the hypotenuse and the other side of the right triangle.

`(1/2) bc sin A = A_t`

`bc = (2A_t)/sin A = 196 / sin (pi/2) = 196`

`ca = 196 / sin B = 296 / sin (pi/8) = 512.1727`

`ab = 196 / sin C = 196 / sin ((3pi)/8) = 212.1489`

`:. ab * bc * ca = (196 * 512.1727 * 212.1489)`

`abc = sqrt (196 * 512.1727 * 212.1489) = 4614.84`

`c = (abc) / (AB) = 4614.84 / 212.1489 = 21.75`

`b = (abc) / (ca) = 4614.84 / 512.1727 = 9`

`a = (abc) / (bc) = 4614.84 / 196 = 23.55`

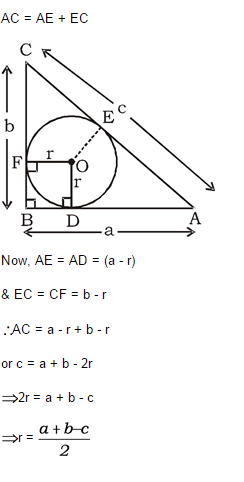
Radius of Incircle

#r_i = (-a + b + c ) / 2 = (9 + 21.75 - 23.55) / 2 ~~ 3.6

Area of Incircle `A_i = pi r_i^2 = pi * 3.6^2 = 40.72` sq units