#"Area of "Delta = A_t = (1/2) a b sin C = (1/2) b c sin A = (1/2) c a sin B#
#"Given " hat A = pi/3, hat B = (5pi)/12, hat C = pi/4#, A_t = 27#
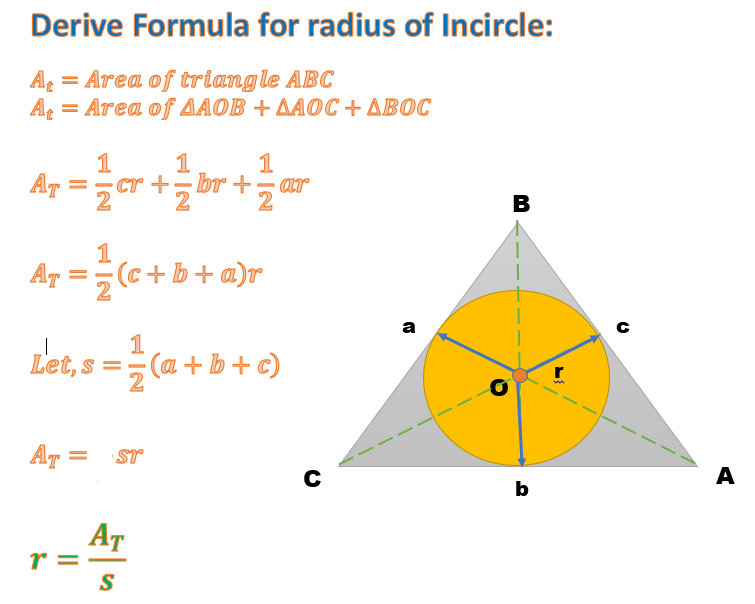 http://mathibayon.blogspot.com/2015/01/derivation-of-formula-for-radius-of-incircle.html#.WzLtzNIza70
http://mathibayon.blogspot.com/2015/01/derivation-of-formula-for-radius-of-incircle.html#.WzLtzNIza70
#a b = (2 A_t) / sin C = 54 / sin (pi/4) ~~ 76.3675#
#b c = (2 A_t) / sin A = 54 / sin (pi/3) = 62.3538#
#c a = (2 A_t) / sin B = 54 / sin ((5pi)/12) = 55.9049#
#a = (a b c) / (b c) = sqrt(76.3675 * 62.3538 * 55.9049) / 62.3538 = 7.8948#
#b = (a b c) / (c a) = sqrt(76.3675 * 62.3538 * 55.9049) / 55.9049 = 9.2291#
#c = (a b c) / (a b) = sqrt(76.3675 * 62.3538 * 55.9049) / 76.3675= 6.7562#
#"Semi-perimeter " = s = (a + b + c) / 2 = 23.8801 / 2 = 11.9401#
#"Radius of inscribed circle " = r = A_t / s = 27 / 11.9401#
#color(indigo)("Area of inscribed circle " = A_i = pi r^2 = pi * (27/ 11.9401)^2 ~~ 16.0643#
 http://mathibayon.blogspot.com/2015/01/derivation-of-formula-for-radius-of-incircle.html#.WzLtzNIza70
http://mathibayon.blogspot.com/2015/01/derivation-of-formula-for-radius-of-incircle.html#.WzLtzNIza70 