Question

A triangle has vertices A, B, and C. Vertex A has an angle of `pi/8`, vertex B has an angle of `(pi)/12`, and the triangle's area is `6`. What is the area of the triangle's incircle?

Answer 1

The area of the incircle is `=1.45u^2`

Explanation:

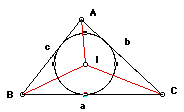
The area of the triangle is `A=6`

The angle `hatA=1/8pi`

The angle `hatB=1/12pi`

The angle `hatC=pi-(1/8pi+1/12pi)=19/24pi`

The sine rule is

`a/(sin hat (A))=b/sin hat (B)=c/sin hat (C)=k`

So,

`a=ksin hatA`

`b=ksin hatB`

`c=ksin hatC`

Let the height of the triangle be `=h` from the vertex `A` to the opposite side `BC`

The area of the triangle is

`A=1/2a*h`

But,

`h=csin hatB`

So,

`A=1/2ksin hatA*csin hatB=1/2ksin hatA*ksin hatC*sin hatB`

`A=1/2k^2*sin hatA*sin hatB*sin hatC`

`k^2=(2A)/(sin hatA*sin hatB*sin hatC)`

`k=sqrt((2A)/(sin hatA*sin hatB*sin hatC))`

`=sqrt(12/(sin(1/8pi)*sin(1/12pi)*sin(19/24pi)))`

`=14.11`

Therefore,

`a=14.11sin(1/8pi)=5.40`

`b=14.11sin(1/12pi)=3.65`

`c=14.11sin(19/12pi)=8.59`

The radius of the incircle is `=r`

`1/2*r*(a+b+c)=A`

`r=(2A)/(a+b+c)`

`=12/(17.64)=0.68`

The area of the incircle is

`area=pi*r^2=pi*0.68^2=1.45u^2`