Question

A triangle has vertices A, B, and C. Vertex A has an angle of `pi/8`, vertex B has an angle of `(pi)/12`, and the triangle's area is `8`. What is the area of the triangle's incircle?

Answer 1

The area of the incircle is `=1.94u^2`

Explanation:

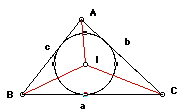
The area of the triangle is `A=8`

The angle `hatA=1/8pi`

The angle `hatB=1/12pi`

The angle `hatC=pi-(1/8pi+1/12pi)=19/24pi`

The sine rule is

`a/sinA=b/sinB=c/sinC=k`

So,

`a=ksinA`

`b=ksinB`

`c=ksinC`

Let the height of the triangle be `=h` from the vertex `A` to the opposite side `BC`

The area of the triangle is

`A=1/2a*h`

But,

`h=csinB`

So,

`A=1/2ksinA*csinB=1/2ksinA*ksinC*sinB`

`A=1/2k^2*sinA*sinB+sinC`

`k^2=(2A)/(sinA*sinB*sinC)`

`k=sqrt((2A)/(sinA*sinB*sinC))`

`=sqrt(16/(sin(pi/8)*sin(pi/12)*sin(19/24pi)))`

`=4/0.246=16.29`

Therefore,

`a=16.29sin(1/8pi)=6.23`

`b=16.29sin(1/12pi)=4.22`

`c=16.29sin(19/24pi)=9.92`

The radius of the in circle is `=r`

`1/2*r*(a+b+c)=A`

`r=(2A)/(a+b+c)`

`=16/(20.37)=0.79`

The area of the incircle is

`area=pi*r^2=pi*0.79^2=1.94u^2`