Question

A wire of length `0.680 m` carries a current of `21.0 A`. In the presence of a `0.470 T` magnetic field, the wire experiences a force of `5.41 N`. What is the angle (less than `90°`) between the wire and the magnetic field?

Answer 1

`alpha=53.13^@`

Explanation:

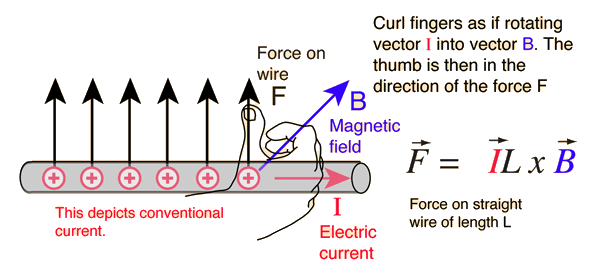
Given

• `L->"Length of the current carrying wire"=0.680m`

• `B->"Applied magnetic field"=0.47 T`

• `I->"Current passing through wire"=21A`

• `F->"Force experienced by the wire"=5.41N`

• `alpha->"Angle between the wire and magnetic field"=?`

Working Formula

• `vecF=vec(IL)xxvecB=ILBsinalpha`

Putting the given values

`5.41=21xx0.680xx0.47xxsinalpha`

`=>sinalpha=5.41/(21xx0.680xx0.47)~~0.8`

`alpha=53.13^@`