A woman at an airport is towing her 20.0-kg suitcase at constant speed by pulling on a strap at an angle θ above the horizontal (see figure). She pulls on the strap with a 35.0-N force, and the friction force on the suitcase is 20.0 N.?
(a) Draw a free-body diagram of the suitcase. (b) What angle does the strap make with the horizontal? (c) What is the magnitude of the normal force that the ground exerts on the suitcase?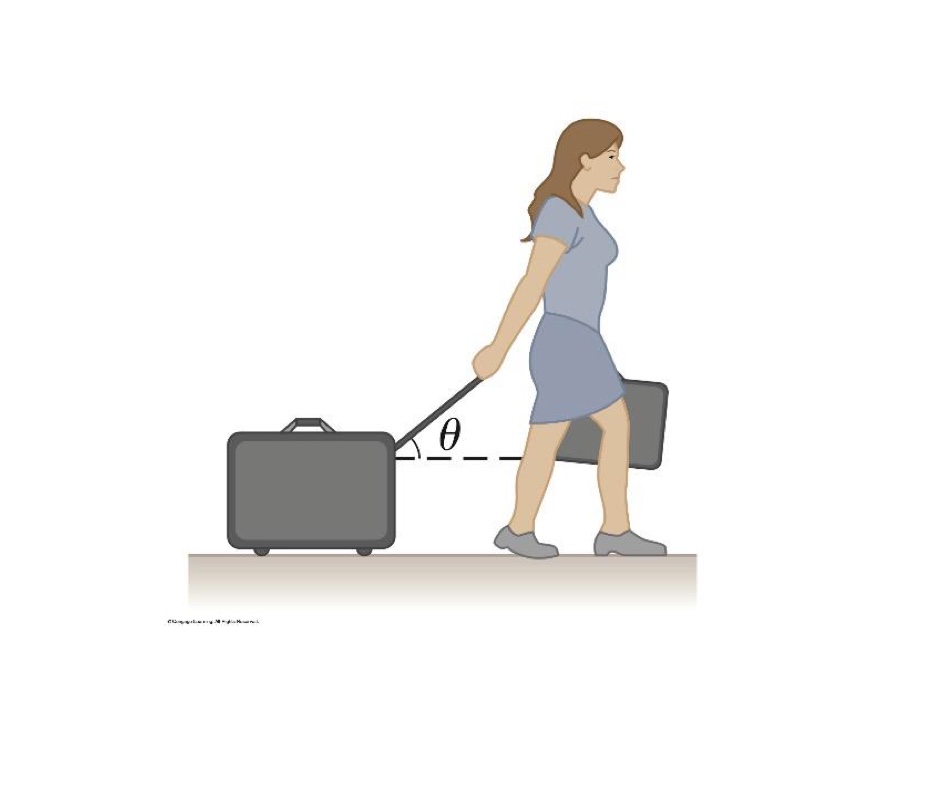
(a) Draw a free-body diagram of the suitcase. (b) What angle does the strap make with the horizontal? (c) What is the magnitude of the normal force that the ground exerts on the suitcase?
1 Answer
b.
c.
Explanation:
a. I will leave this task to you. My work on b and c should give you clues on what the free-body diagram needs to include.
b. Since she is going at constant speed, none of her force is going to acceleration and none of the friction is making her decelerate. Therefore we can say that the horizontal component of her 35.0 N is equal to, but opposite, the friction.
Solving for
c. The weight of the suitcase is
But that is not the answer to the question. The vertical component of her 35.0 N is partially lifting the suitcase. The value of the partial lift is
That leaves
I hope this helps,
Steve

