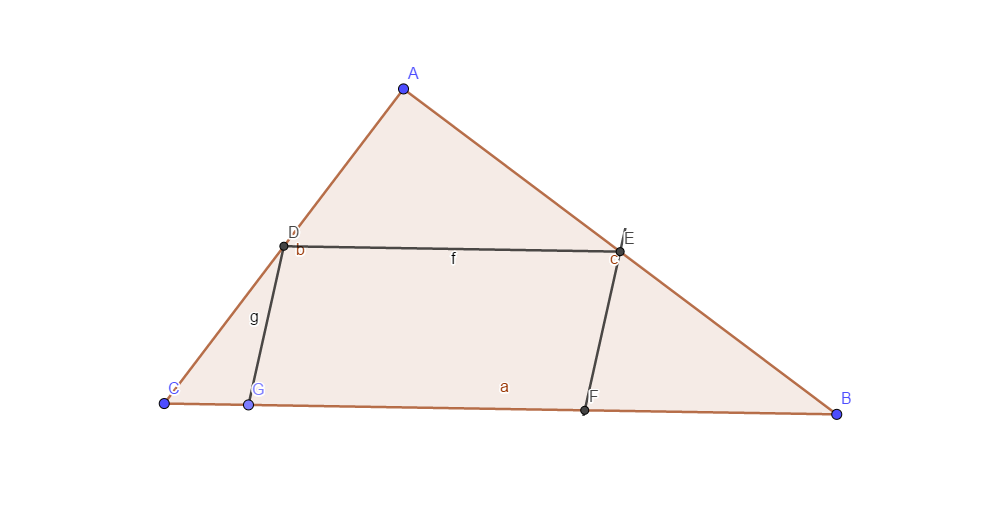
ABC is a triangle with D and E as the mid points of the sides AC and AB respectively. G and F are points on side BC such that DG is parallel to EF. Prove that the area of triangle ABC=#2xx# area of quadrilateral DEFG.?
2 Answers
see explanation.
Explanation:
Let
let
given
let
let
draw a line joining
As
similarly,
let
let
given that
Hence,
see explanation.
Explanation:
Solution 2:
Given that
let
let
given
