ABC is a triangle whose sides AB = 6 cm, BC = 8 cm and AC = 12 cms. D is such a point situated on AC that angle ADB = angle ABC. Find the length of BD ?
1 Answer
Jan 7, 2017
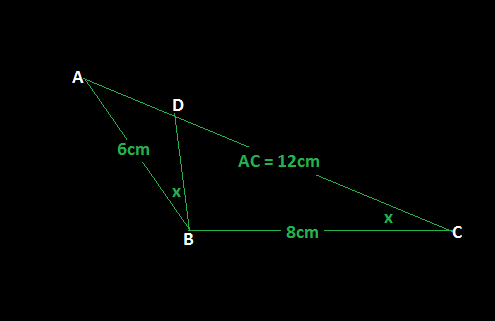
In
#/_BAD=/_BAC ("common")# -
#/_ADB=/_ABC ("given")# -
#/_ABD=/_ACB ("remaining")#
So
Hence

