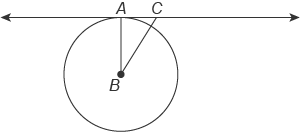
AC←→ is tangent to the circle with center at B. The measure of ∠ACB is 58°. What is the measure of ∠ABC ?
3 Answers
Explanation:
angleBAC=90^@to(" angle between tangent and radius")
"angle sum of "triangleABC=180^@
rArrangleABC=180^@-(90+58)^@=32^@
58°
Explanation:
The answer is given in the question
Explanation:
Let's start out by laying out what we know:
1)
2) Since
3)
Do you see that little triangle that's inside the circle? Well we know that the angles of a triangle add up to
Let's substitute into this equation since we know some of the angles:


