Adjacent sides of a parallelogram have lengths 12.5 cm and 8 cm. The measure of the included angle is 40º. Find the area of the parallelogram to the nearest tenth of a cm?

Question

1718 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-25T06:26:11

Please read the explanation.

#" "#
Adjacent sides of a Parallelogram and the included angle are given.

Draw a sketch:

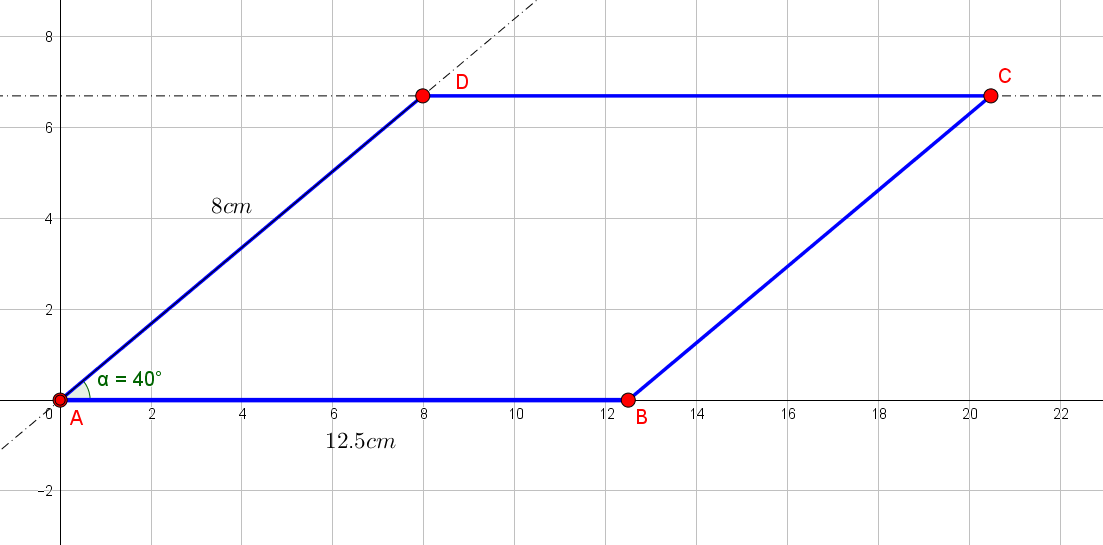
enter image source here

#ABCD# is the parallelogram with

#bar(AB)="12.5 cm" and bar(AD)="8 cm"#

#/_BAD = 40^@#

Altitude #DE#, a perpendicular line segment is drawn through point #D# to the base #AB#.

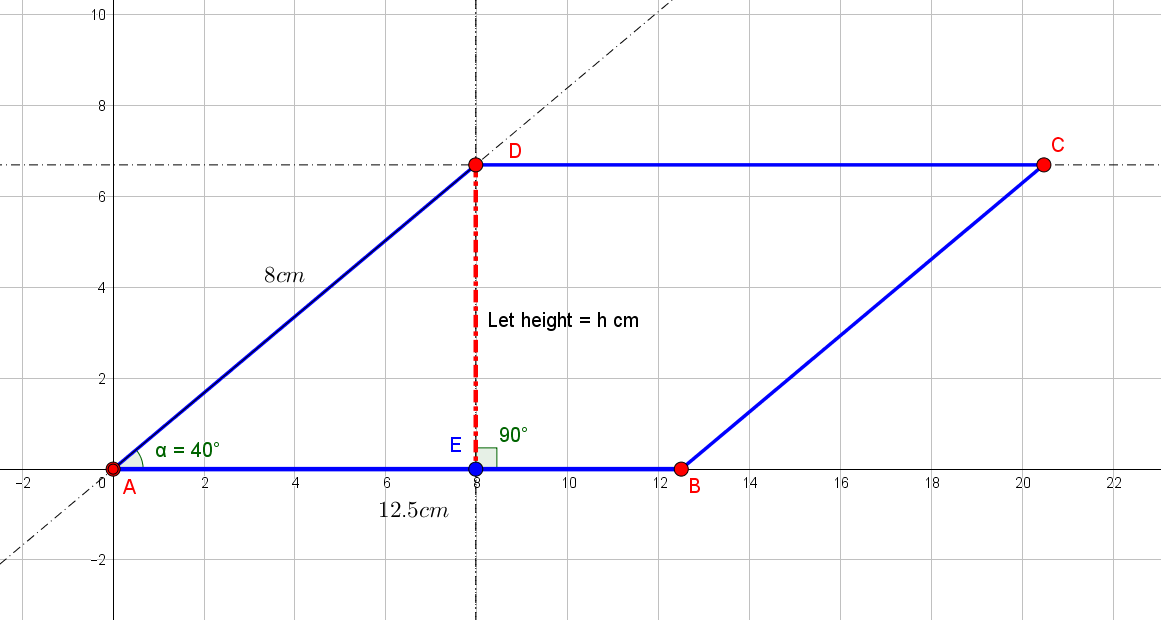
enter image source here

Let #bar(DE)= "h cm"#.

Observe that #/_AED = 90^@# with #/_A=40^@#

#/_AED# is a right-triangle.

Area of the Parallelogram #color(blue)(ABCD = AB*DE=base * h#

Observe that

#h/(AD) = sin(theta)#

#h/(AD) = sin(40^@)#

#h=AD*Sin(40^@)#

#h=8*sin(40^@)#

#h~~8*(0.64278760968)#

#h~~5.142301#

Hence, Height of the Parallelogram #DE ~~ "5.142301 cm"#

Hence,

Area of the Parallelogram #=Base * Height#

#rArr (12.5)*(5.142301)#

Hence,

Area of the Parallelogram #ABCD ~~ "64.3 cm"^2#.