Am I wrong about this?
Many people on here and in text books say that when an equation doesn't have real roots, they refer to them as complex roots.
If all numbers can be written in the form a+bia+bi , this obviously means real or imaginary numbers, and these are called complex numbers, then it must be wrong to refer to a complex number as if it was always an imaginary number. So saying the roots of an equation are complex roots, seems to me to be wrong, or is it me who is wrong. This has been bugging me for a long time.
Many people on here and in text books say that when an equation doesn't have real roots, they refer to them as complex roots.
If all numbers can be written in the form
3 Answers
Yes, you are correct. There is a difference between an imaginary number and a complex number.
It is correct to refer to an imaginary number as a complex number, but incorrect to refer to a complex number as an imaginary number.
Explanation:
I think people become very lazy in speech when it comes to referring to quantities as imaginary or complex.
A complex number is a number that contains a real part and an imaginary part. As you have shown, it is commonly written as:
In the case that
Similarly, most numbers that we deal with on a daily basis have
With these ideas in mind, imaginary numbers are a subset of complex numbers. So are real numbers. Complex numbers are mathematically the most general type of number. I have included a picture like the one below to illustrate:
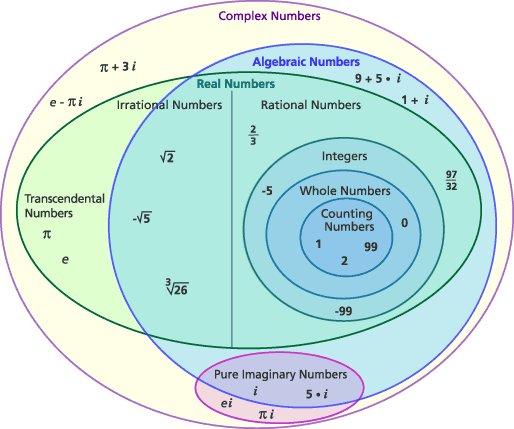 stackexchange
stackexchange
Hence, it is correct to refer to an imaginary number as a complex number, but incorrect to refer to a complex number as an imaginary number.
Your understanding of complex numbers is absolutely correct...I can't quite understand where the problem lies
Explanation:
When the textbook refers to a equation that yields an imaginary answer as it having complex roots, it is absolutely correct as well. Because as you said, a complex root contains an imaginary and a real part, so when your textbook says that the solution to the equation is a complex number instead of just imaginary, they are accounting for that real part to the imaginary solution you might get.
For example, when you do the quadratic formula and the number and the discriminant is negative, you have two parts to your solution, a real number
Yes you are correct, all numbers can be written in
Explanation:
If we want to think of this from a logic standpoint, the set of complex numbers is the super-set of the two subsets real numbers and imaginary numbers. All real numbers and imaginary numbers are complex numbers.
When we refer to imaginary numbers, more often than not they are complex. When we refer to real numbers, we can stay away from the complex definition for the most part. Therefore, it has become somewhat standard to associate complex numbers with imaginary numbers. You are, however, correct; it is improper to refer to a complex number as only imaginary.
Bottom line, you're correct, but cut your teachers/textbooks some slack, the world of mathematics gets lazy saying the same thing over and over again and shortcuts abound to reduce time and effort. If the roots are only real then we don't bother with the word "complex." If the roots have an imaginary part, are entirely imaginary, or have the possibility of being imaginary then we care about placing the word "complex" somewhere in our reasoning.
The reason for this methodology beyond the scope of your question but it has to do with graphing complex numbers themselves, with their real part on one axis and their imaginary part on the other.



