An airplane flies on a course of 110° at a speed of 1200 km/h. How far east of its starting point is it after 2 h?

Question

4303 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-01T12:02:42

#2255.3# km. ( 1 d.p. )

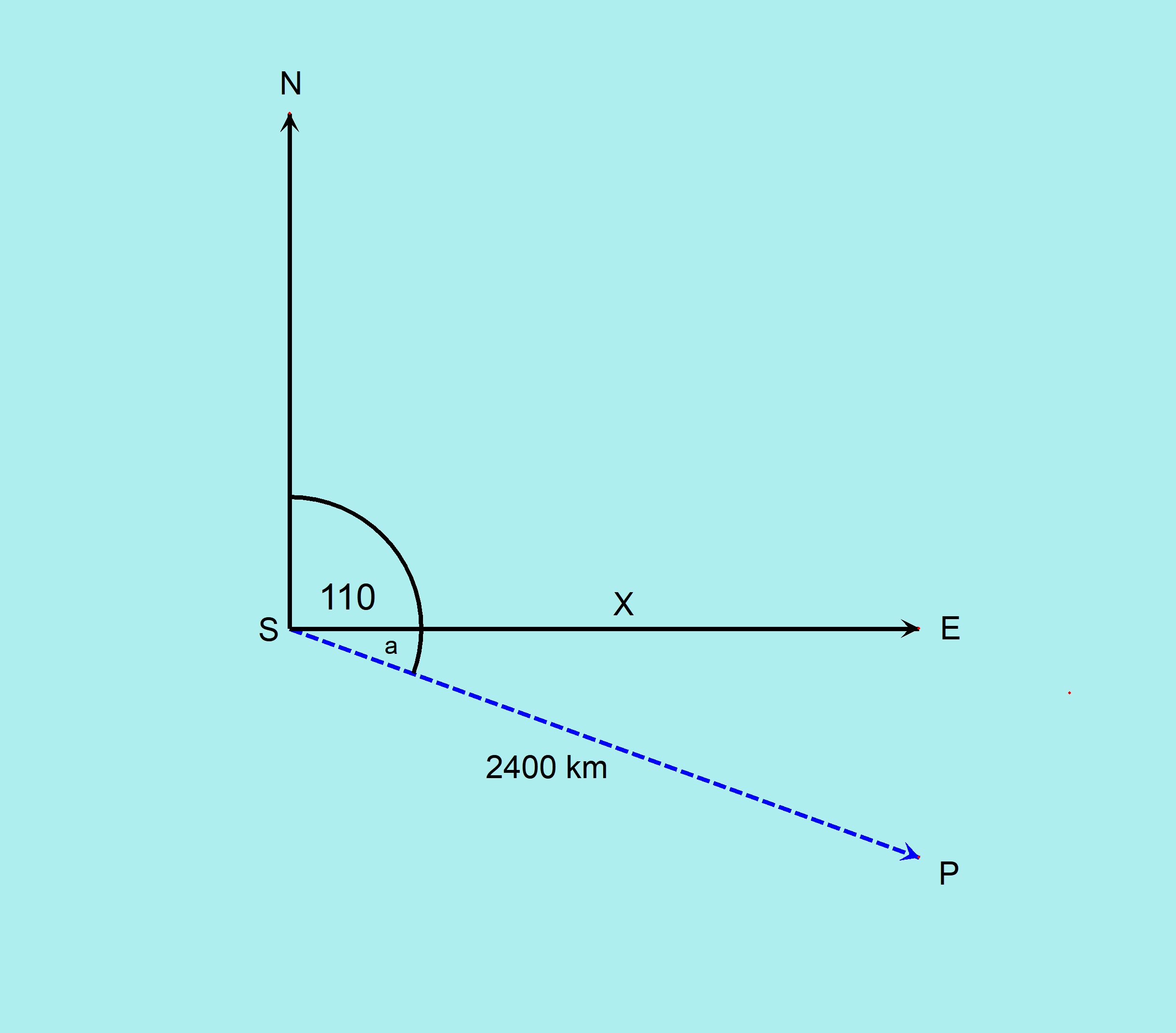
enter image source here

From the diagram.

If the plane starts a point S on a bearing of #110^@#, travelling at 1200 km/h, after 2 hrs it will be at point P.

Distance from S to P:

#2xx1200# km/h = 2400 km.

If we are looking for the distance due east the plane is after 2 hrs, this is marked as X on the diagram.

We can find this distance using the cosine ratio. We first need to find angle a.

#a=110^@-90^@=20^@#:

#:.#

#cos(a)="adjacent"/"hypotenuse"=X/2400#

#cos(20^@)=X/2400#

Rearanging:

#X=2400cos(20^@)=2255.3# km. ( 1 d.p. )