An airplane is heading north at an airspeed of 700 km/hr, but there is a wind blowing from the northeast at 40 km/hr. The plane will end up flying ______(?)degrees off course. The plane's speed relative to the ground will be _____(?)km/hr.

Give your answers accurate to the nearest tenth.

1 Answer
Michael
Mar 2, 2018

#sf(N2.4^@W)# or Bearing #sf(357.6^@)#

#sf(672.2color(white)(x)"km/hr")#

Explanation:

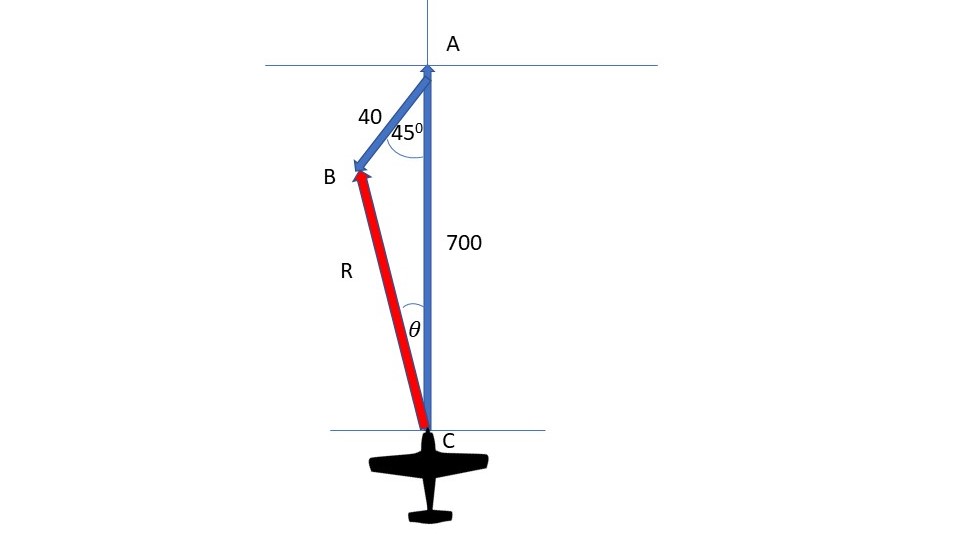
MF Docs

The red arrow shows the resultant vector. We have a Side Angle Side triangle ABC so can use The Cosine Rule:

#sf(a^2=b^2+c^2-2"bc"cosA)#

This becomes:

#sf(R^2=700^2+40^2-(2xx700xx40xxcos45))#

#sf(R^2=491,600-39,597.9)#

#sf(R=672.3color(white)(x)"km/hr")#

This is the groundspeed of the aircraft.

To find #sf(theta)# we can use The Sine Rule:

#sf(sinC/c=SinA/a)#

This becomes:

#sf(sintheta/40=sin45/672.3)#

#sf(sintheta=0.04207)#

#sf(theta=2.41^@)#

This is known as the drift angle and is the correction the pilot should apply to remain on course.

The heading is the direction the aircraft's nose is pointing which is #sf(000^@)#.

The track is the actual direction over the ground which is #sf(357.6^@)#

An alternative method to this would be to separate each vector into vertical and horizontal components and add.

The resultant can be found using Pythagoras.

Related questions
Impact of this question
92632 views around the world
You can reuse this answer
Creative Commons License