An electron is revolving round a proton, producing a magnetic field of #16 weber/m^2# in a circular orbit of radius #1Å#. Its angular velocity is?
1 Answer
Electron revolving round a proton constitute flow of current in a circular ring of radius
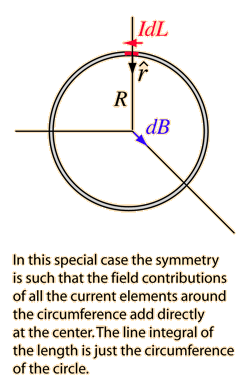
Let an infinitesimal length element
#vec(dB)=(mu_0Ivec(dL)xxhatr)/(4piR^2)#
where#mu_0# is the magnetic constant or the permeability of free space#=4pixx10^-7Hm^-1#
We see that the angle between each current element and radial unit vector
#B=(mu_0I)/(4piR^2)oint " "dL#
We also see that for all points along the path and the distance to the center is constant in such a case line integral is equal to the circumference of the circle.
#=>B=(mu_0I)/(4piR^2)2piR#
#=>B=(mu_0I)/(2R)# .....(1)
Current
If
#I=ef#
Now
#omega=2pif#
Hence current in terms of angular velocity is
#I=exxomega/(2pi)#
Inserting given values in (1) we get
#16=(4pixx10^-7xx(1.60 × 10^-19)xxomega/(2pi))/(2xx10^-10)#
#=>omega=(16xx10^-10)/(10^-7xx(1.60 × 10^-19))#
#=>omega=10^17" radian"cdot" s"^-1#
