An isosceles trapezoid MNPQ with QP=12 and measure of angle M = 120 degrees has bisectors of angles MQP and NPQ that meet at point T on line MN. What is the perimeter of MNPQ?
1 Answer
Explanation:
First a discussion about the internal angles of the isosceles trapezoid.
Consider Figure 1
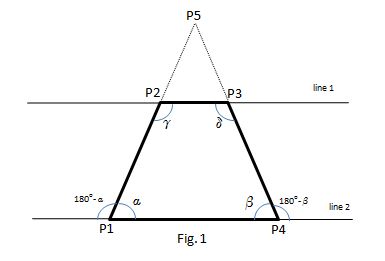
In a isosceles trapezoid, if its equal sides are extended, we get an isosceles triangle whose base is the bigger base of the trapezoid. In a isosceles triangle, the angles with the base,
In the present case,
Discarding impossible case
Consider Figure 2
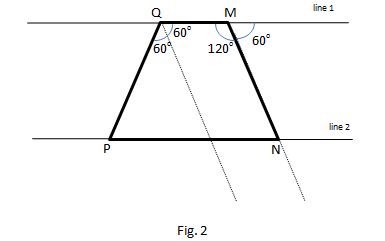
Since the problem doesn't present a picture, there would be two possibilities of configuration. Case 1 in which the segment MN forms the trapezoid's smaller base and Case 2 in which the segment QM forms the smaller base.
But the second case is impossible since then the angle
Resolving the problem for Case 1
Consider Figure 3
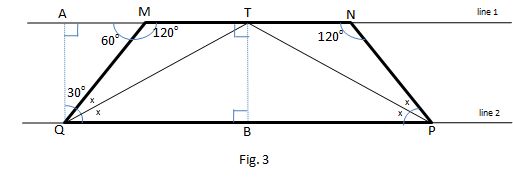
From the discussion of the internal angles of the trapezoid and from the conditions of the problem, we know that
Drawing a line from the vertex Q and perpendicular to the segment MN, it intercepts the line in which the segment MN stands in point A
Drawing a line from the point T and perpendicular to the segment MN, it intercepts the line in which the segment PQ stands in point B. Using the rule angle-side-angle, we can see the triangles MQT and NPT are congruents, then, using the rule side-angle-side, we can see that the triangles BQT and BPT are congruent what means that
Since
Since AQBT is a rectangle,
In the triangle AQT
In the triangle AMQ

