An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from (5 ,1 ) to (3 ,2 ) and the triangle's area is 12 , what are the possible coordinates of the triangle's third corner?
1 Answer
Two possibilities:
Explanation:
Refer to the figure below
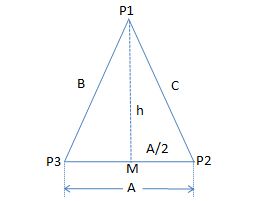 I created this figure using MS Excel
I created this figure using MS Excel
It's known that:
It's asked
Now we could use the equations of the distance between 2 points to determine
line
Distance between a point and a line
So, making
We get two equations:
(I)
(II)
Since
line
Finding the two possible answers (by combining [2] and [4] or [3] and [4]):
(I)
2x-6.5=-x/2+15.5 => 2.5x=22=> x=8.8
->y=2*8.8-6.5 => y=11.1
=> (8.8,11.1) (II)
2x-6.5=-x/2-8.5 => 2.5x=-2 => x=-0.8
->y=2*(-0.8)-6.5 => y=-8.1
=> (-0.8,-8.1)
Checking the results:
Notice that
and
Notice also that
(testing result I)
(testing result I)
(Try result II)
As it should be: all checked

