An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from #(7 ,1 )# to #(2 ,9 )# and the triangle's area is #32 #, what are the possible coordinates of the triangle's third corner?

Question

1612 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-25T16:16:51

# (1825/178, 765/89) or( -223/178, 125/89)#

We relabel in standard notation: #b=c#, #A(x,y)#, #B(7,1),# #C(2,9)#. We have #text{area}=32#.

The base of our isosceles triangle is #BC#. We have

#a=|BC| =sqrt{5^2+8^2}=sqrt{89}#

The midpoint of #BC# is #D=((7+2)/2, (1+9)/2) = (9/2, 5)#. #BC#'s perpendicular bisector goes through #D# and vertex #A#.

#h=AD# is an altitude, which we get from the area:

#32 = \frac 1 2 a h = 1/2 \sqrt{89}\ h #

#h = 64/sqrt{89}#

The direction vector from #B# to #C# is

#C-B=(2-7,9-1)=(-5,8)#.

The direction vector of its perpendiculars is #P=(8,5)#, swapping the coordinates and negating one. Its magnitude must also be #|P|=sqrt{89}#.

We need to go #h# in either direction. The idea is:

# A = D \pm h P /|P| #

# A =(9/2,5) \pm (64/sqrt{89}) {(8,5)} / \sqrt{89}#

# A =(9/2,5) \pm 64/89 (8,5) #

#A = (9/2 +{ 8 (64)}/89, 5 + {5(64)}/89 ) or ##A = (9/2 - { 8 (64)}/89 , 5 - {5(64)}/89) #

# A=(1825/178, 765/89) or A=( -223/178, 125/89)#

That's a bit messy. Is it right? Let's ask Alpha.

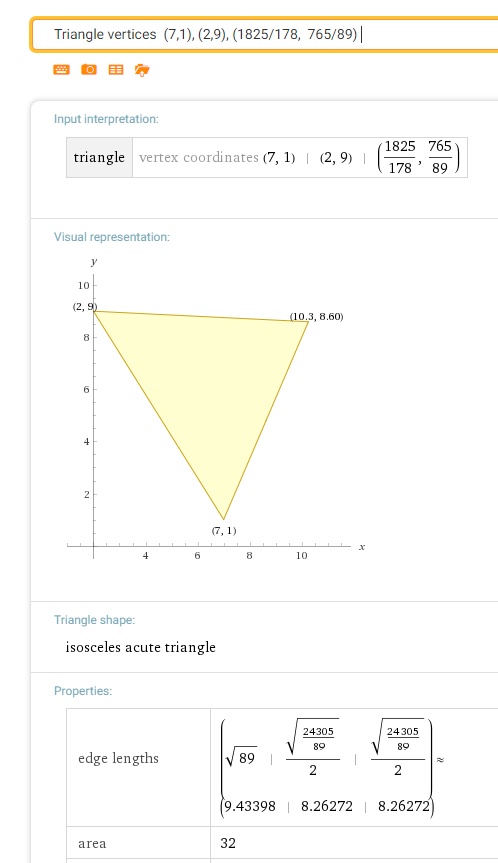
enter image source here

Great! Alpha verifies its isosceles and the area is #32.# The other #A# is right too.