An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from #(1 ,4 )# to #(5 ,8 )# and the triangle's area is #15 #, what are the possible coordinates of the triangle's third corner?
2 Answers
Coordinates of third vertex A of equilateral triangle ABC is
Explanation:
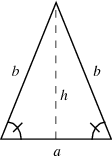
Length of side BC =
Height
Length of side b = c = sqrt((a/2)^2 + h^2)#
Coordinates of center point of BC = D is ((5+1)/2, (8+4)/2) = (3,6)#
Slope of line segment BC
Slope of altitude AD = -(1/m) = -1#
Equation of AD is
Slope of line BA = m1 = h / b = 5.3033 / 6.01 = 0.8824#
Equation of line BA is
Solving Eqns (1), (2) we get the coordinates of the third vertex A.
Coordinates of third vertex A of equilateral triangle ABC is
Explanation:
Bearing
Bearing A-B
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Check:-
Bearing

