Question

An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from `(2 ,5 )` to `(8 ,7 )` and the triangle's area is `12`, what are the possible coordinates of the triangle's third corner?

Answer 1

The possible points are: `(3.8, 9.6)` and `(6.2, 2.4)`

Explanation:

The length of side "a" is:

`a = sqrt((8 -2)^2 + (7 - 5)^2) = sqrt(40) = 2sqrt(10)`

The area of a triangle is:

`"Area" = (1/2)"Base"xx"Height"`

Using side "a" as the base of the triangle and the given area, we can compute the height:

`12 = (1/2)2sqrt(10)xx"Height"`

`"Height" = 12/sqrt(10)`

Think of the height as the radius of a circle upon which the two possible points must lie:

`(x - h)^2 + (y - k)^2 = (12/sqrt(10))^2`

Because the triangle's other two sides are the same length, the center of this circle must be the midpoint between the points #(2, 5) and (8, 7):

`h = 2 + (8 - 2)/2 = 5 and k = 5 + (7 - 5)/2 = 6`

Substitute into the equation of the circle:

`(x - 5)^2 + (y - 6)^2 = (12/sqrt(10))^2" [1]"`

The two points must, also, lie on a line that is perpendicular to side "a"; the slope, m, of this line is:

`m = (2 - 8)/(7 - 5) = -6/2 = -3`

Using, this slope, the center point, and the point-slope form of the equation of a line, we write the equation upon which the two points must lie:

`y = -3(x - 5) + 6" [2]"`

Here is a graph of the equation [1], equation [2] and the two given points:

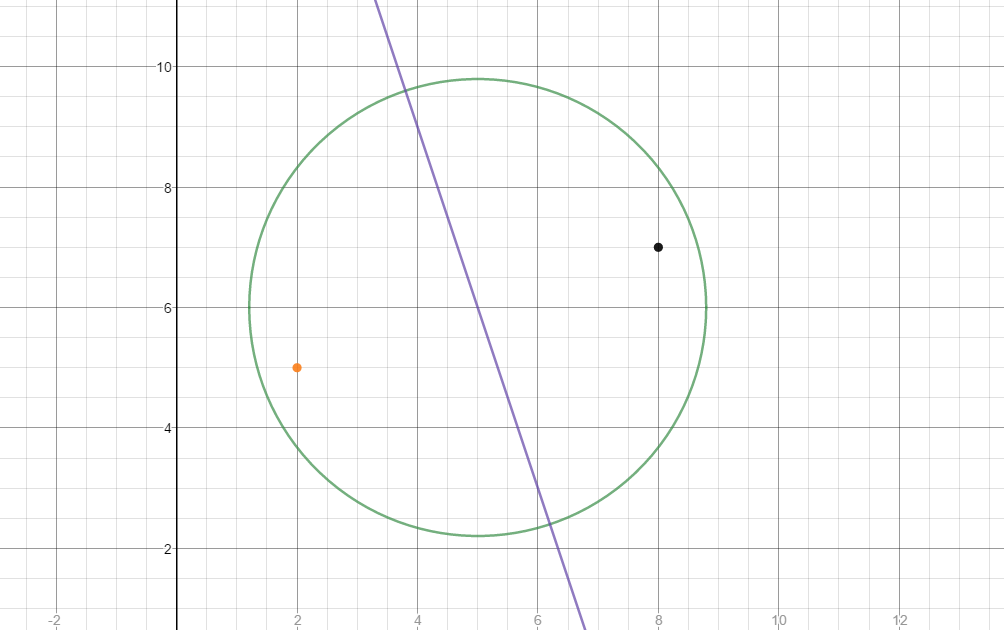
Substitute the right side of equation [2] into equation [1]:

`(x - 5)^2 + (-3(x - 5) + 6 - 6)^2 = (12/sqrt(10))^2`

`(x - 5)^2 + (-3(x - 5))^2 = (12/sqrt(10))^2`

`(x - 5)^2 + 9(x - 5)^2 = (12/sqrt(10))^2`

`(x - 5)^2 + 9(x - 5)^2 = 144/10`

`10(x - 5)^2 = 144/10`

`(x - 5)^2 = 144/100`

`x - 5 = +-12/10`

`x = 5 +-12/10`

`x = 3.8 and x = 6.2`

To obtain the corresponding y values, substitute these x values into equation [2]

`y = -3(3.8 - 5) + 6` and `y = -3(6.2 - 5) + 6`

`y = 9.6 and y = 2.4`