#"the velocity of an object is defined as total distance covered in "#
#"unit time. Velocity is a scalar quantity. It has a magnitude but "#
#"no direction."#
#" average velocity of an object is calculated using formula:"#
#v_a=("total distance covered")/("given time interval")#
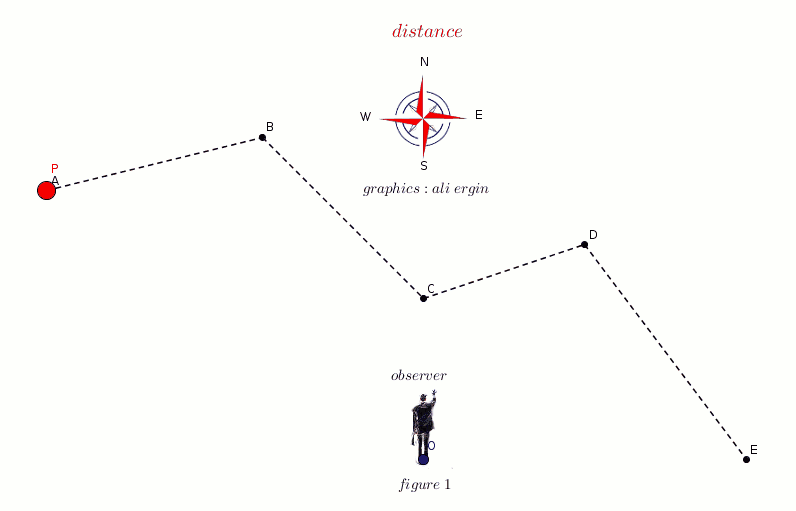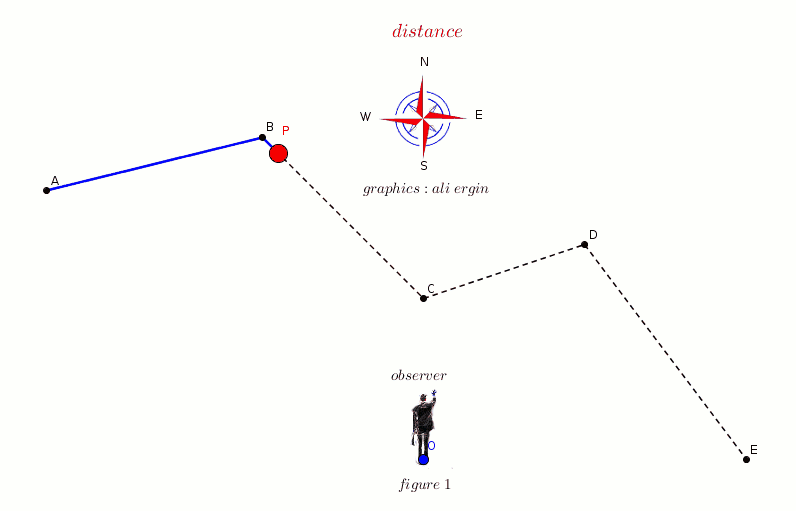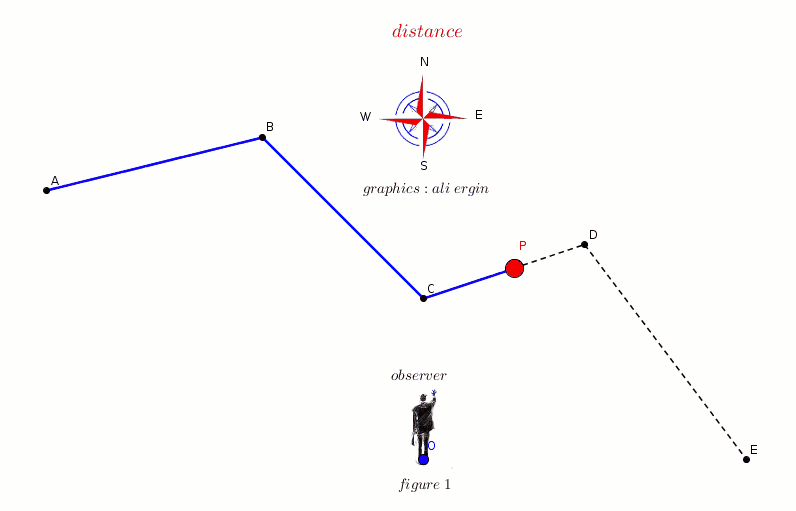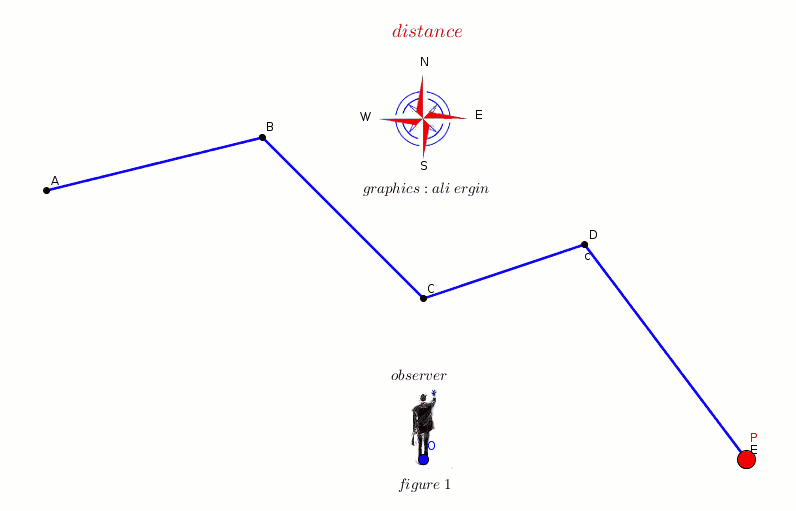
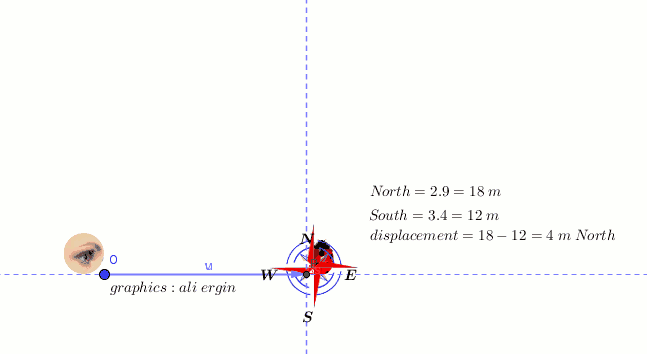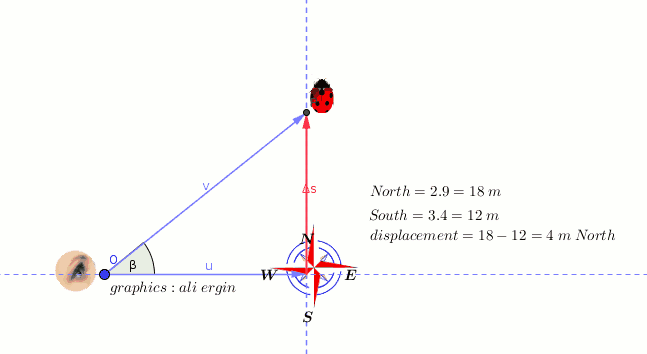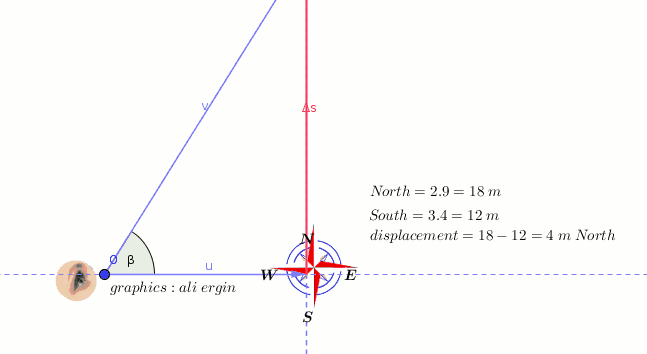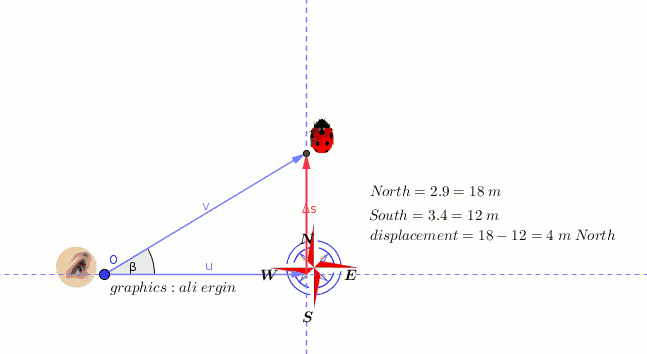
#"figure 1 shows the distance of object P"#
#"distance=AB+BC+CD+DE#
#"northward :"x_N=2*9=18 " "m"#
#"southward :"x_S=4*3=12 " "m#
#"total distance covered: " x=18+12=30 " "m#
#"given time interval : "Delta t=9+3=12 " "s#
#v_a=30/12=15/6=5/2=2.5" "m/s#
#"Velocity is defined as net displacement of an object in unit time"#
#"Velocity is a vector quantity. it has both a magnitude and a direction"#
#v_a=("net displacement of object")/("time interval")#
#"displacement is a vector quantity ."#
#"it is calculated either Pythagoras or cosine law".#
#"net displacement="18-12=4" m"#
#v_a=4/(9+3)#
#v_a=4/12=1/3 " m/s#





