Question

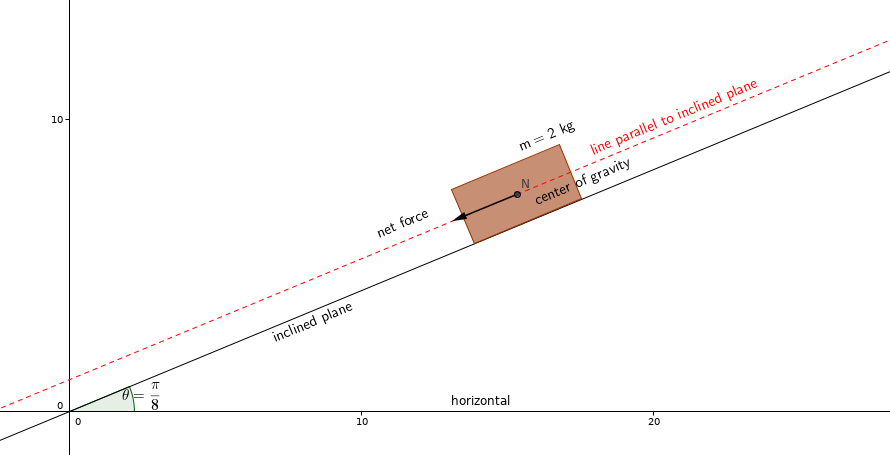
An object with a mass of `2 kg` is on a plane with an incline of `pi/8`. If the object is being pushed up the plane with `8 N` of force, what is the net force on the object?

Answer 1

`"please see the explanation section."`

Explanation:

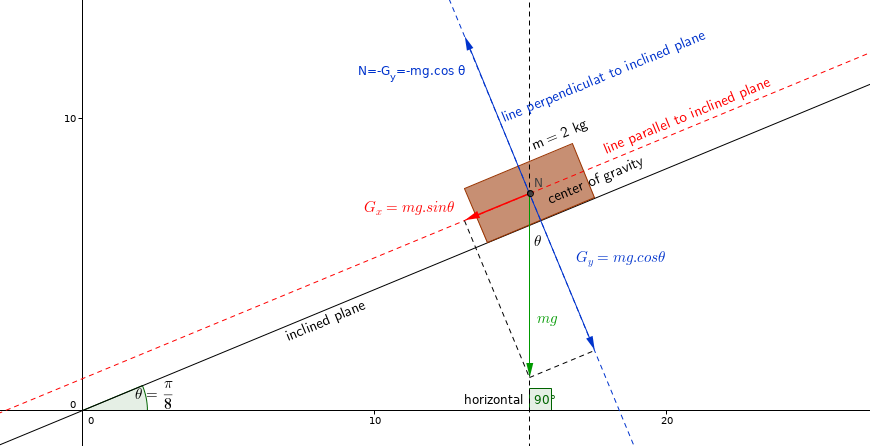
• drawing a free-body diagram will make it easier to understand.
• blue and red dotted lines will be useful to separate the weight of the object from the components.

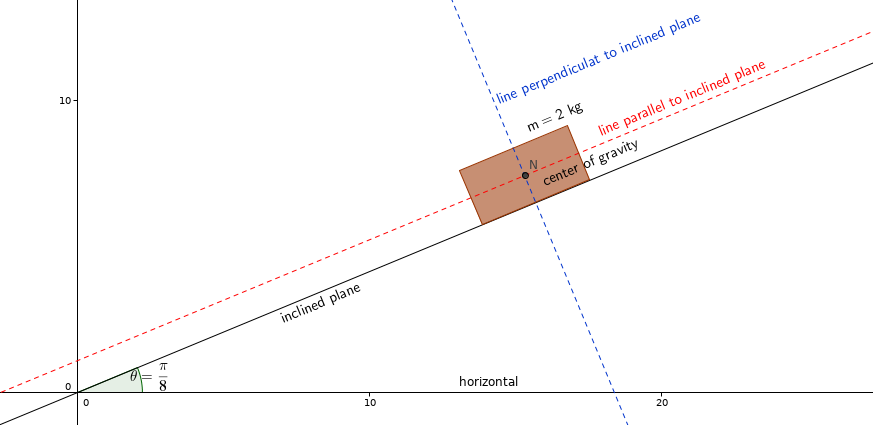
• The vector drawn with green symbolizes the weight of the body.

`G=mg=2*9.81=19.62N`

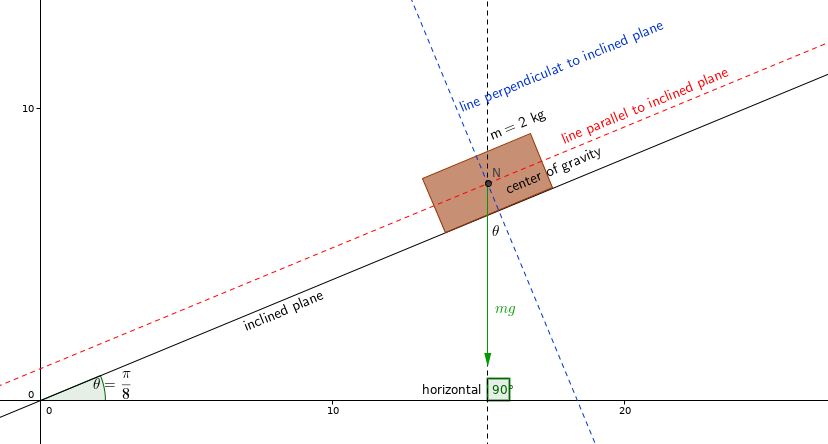
• we now have to find the components of the weight on the red and blue axes.

`G_x=mg*cos theta=2*9.81*cos(pi/8)=18.13 N`

`G_y=mg*sin (theta)=2.9.81*sin (pi/8)=7.51N`

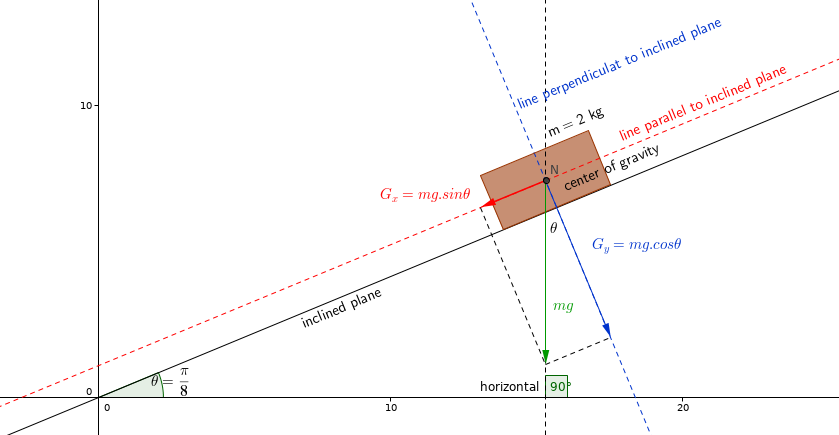
• The blue vector is acting vertically. We know that the inclined plane will react against the effect(Newton's third law).

`N=-G_y=-mg*cos theta`
`N+(-G_y)=0`

• now,let's draw the Force of 8 N and Simplify the look of the diagram.

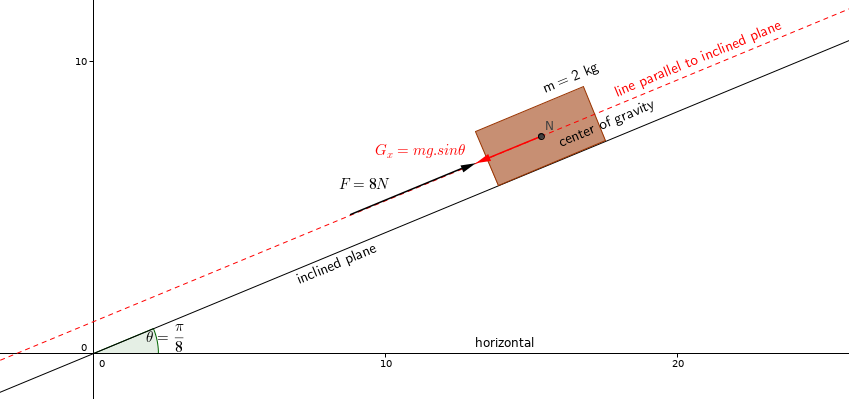
• we need to find the sum of the black and red vectors.

`F_("net")=G_x-F`

`F_("net")=18.13-8`

`F_("net")=10.13N`