An object with a mass of 24 kg is hanging from an axle with a radius of 16 m. If the wheel attached to the axle has a radius of 48 m, how much force must be applied to the wheel to keep the object from falling?
2 Answers
The force is
Explanation:
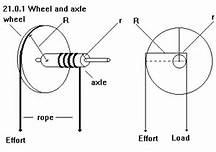
The load is
The radius of the axle is
The radius of the wheel is
The effort is
The acceleration due to gravity is
Taking moments about the center of the axle
The force is
Explanation:
Did you know that units of measurement can be manipulated in the same way that numbers can. If you are ever not sure what to do with the numbers look at what you have to do to the units to give you your target.
The mass of 24 kg converted to downward force in Newtons is:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Presenting opposing forces about the shaft centre line of the shaft as if it is a fulcrum we have:
 Tony B
Tony B
If this condition is not 'in equilibrium' (all balanced out) then the system would be in motion.
Taking moments about the fulcrum
But force is measure in Newtons by changing the units of measurement we have:
Divide both sides by
But


