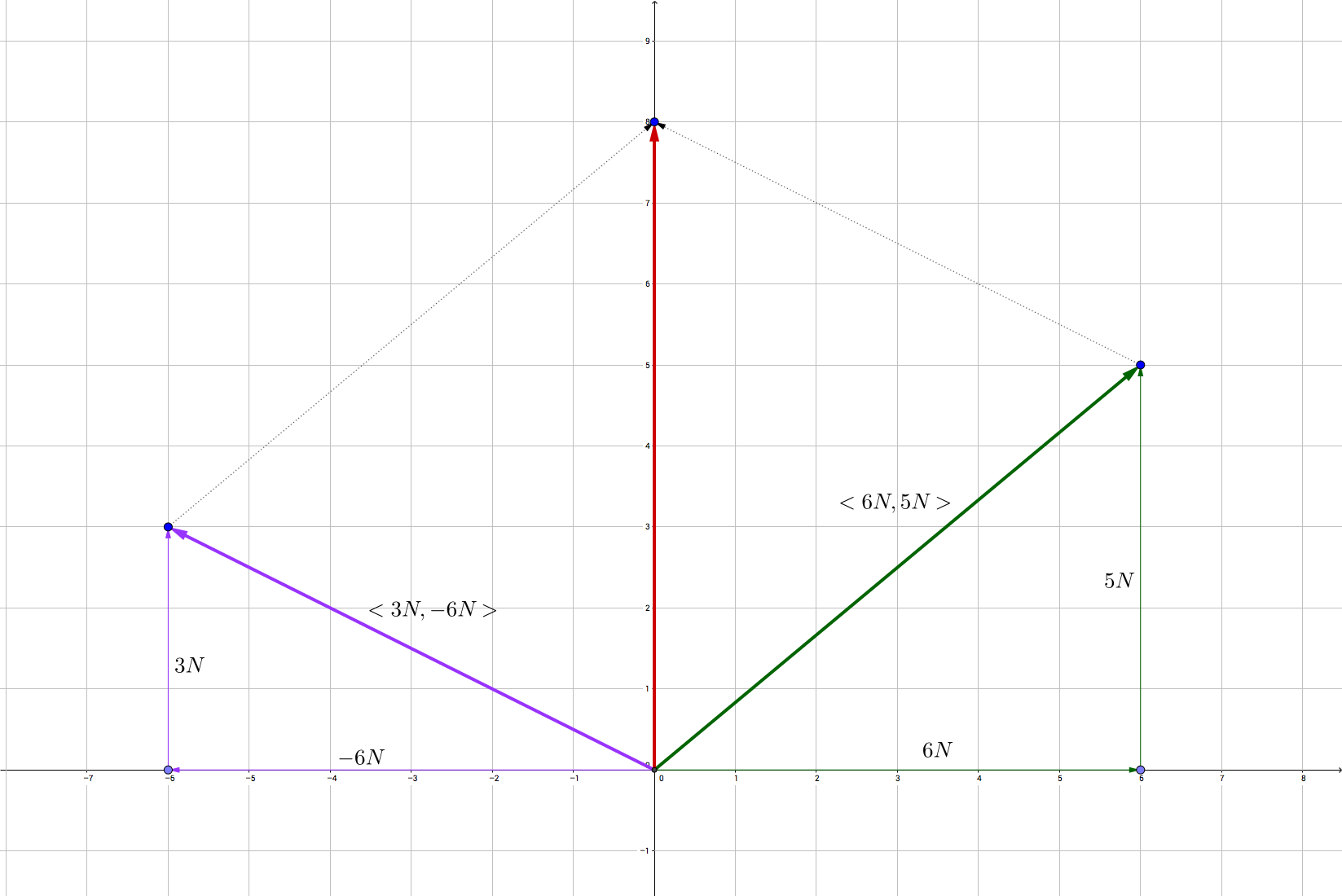
An object with a mass of #4 kg# is acted on by two forces. The first is #F_1= < -6 N , 3 N># and the second is #F_2 = < 6 N, 5 N>#. What is the object's rate and direction of acceleration?
1 Answer
Jun 8, 2016
The acceleration is
Explanation:
When you want to sum two vectors in classical mechanics, it is enough if you sum them component by component.
The final vector is
The length of a vector is given by
that of our vector is
Then the force is with a magnitude of 8N and the acceleration is given by
The direction is given by
This of course is a problem because we cannot divide by zero. On the other hand we know that the arctan is singular when the angle is