An object with a mass of #4 kg# is hanging from a spring with a constant of #3 (kg)/s^2#. If the spring is stretched by # 12 m#, what is the net force on the object?
2 Answers
Jul 11, 2017
The net force is
Explanation:
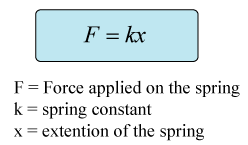
The mass is
The spring constant is
The extension is
Resolving in a vertical direction
The net force is
Jul 11, 2017
The net force should ideally be zero
Explanation:
The object hanging by the spring is acted on by two forces.The gravitational force pulls its down while the spring resists this.
The force exerted by spring is given by Hooke's law as follows
The gravitational force is given by the equation
In a state of equilibrium


