An object with a mass of #4 kg# is on a plane with an incline of #pi/12 #. If the object is being pushed up the plane with # 1 5 N # of force, what is the net force on the object?
1 Answer
Explanation:
Begin by drawing a force diagram, then use this diagram to construct statements for the net force.
I will assume a frictionless surface. This means that the forces acting on the object include the normal force, the force of gravity, and the pushing force. We can draw a diagram:
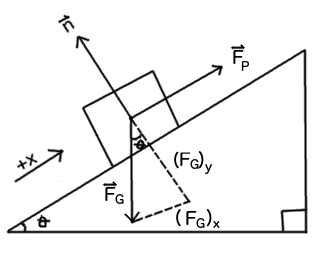
where
#vecn# is the normal force,#vecF_P# is the pushing force, and#vecF_G# is the force of gravity. Note that I have defined up the ramp as the positive direction. This is how we will decide whether the forces are positive or negative later. I'll drop vector arrows from now on.
#(F_(n e t))_x=sumF_x=F_p-(F_G)_x=ma_x#
#(F_(n e t))_y=sumF_x=n-(F_G)_y=ma_y#
Because the object is not accelerating vertically (not moving up or down), we know that
While both the normal force and pushing force are completely perpendicular and parallel (respectively), the force of gravity will have to be broken up into both its parallel and perpendicular components. We can do this using basic trigonometry.
We see, for the inner triangle, that
#vecF_(n e t)=(F_(n e t))_x=sumF_x=F_p-(F_G)sintheta=ma_x#
#=>vecF_(n e t)=F_p-(F_G)sintheta#
#=>=F_p-mgsintheta#
Using that
#vecF_(n e t)=15N-(4kg)(9.81m/s^2)sin(pi/12)#
#=4.8N#
Since this is a positive value, we know that the direction of the net force is up the ramp, since this is the direction we defined as positive and we kept our signs consistent throughout. This makes sense, as the pushing force is greater than the force of gravity which opposes it. Therefore, we expect the object to be moving up the ramp against the force of gravity.

