An object with a mass of #5 kg# is on a plane with an incline of #pi/8 #. If the object is being pushed up the plane with # 8 N # of force, what is the net force on the object?
1 Answer
Explanation:
We are given the following information:
#|->m=5"kg"# #|->theta=pi/8# #|->F_p=8"N"#
A diagram of the situation:
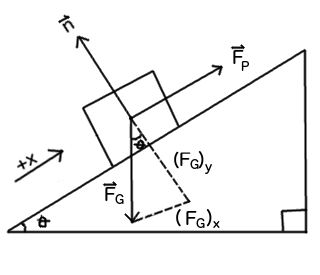
Where
#vecn# is the normal force,#vecF_G# is the force of gravity, decomposed into its parallel and perpendicular components, and#vecF_p# is the pushing force.Note: I will assume a "frictionless" incline based on the information provided.
Let's define up the incline as positive.
We can calculate the net force on the object by summing the parallel (x, horizontal) and perpendicular (y, vertical) components of our forces. We have:
#F_(x" net")=sumF_x=F_p-(F_G)_x=ma_x#
#F_(y" net")=sumF_y=n-(F_G)_y=ma_y#
We can assume dynamic equilibrium vertically, where
#color(darkblue)(F_(x" net")=F_p-(F_G)_x)#
#color(darkblue)(F_(y" net")=0#
Since we're given
#sin(theta)="opposite"/"hypotenuse"#
#=>sin(theta)=(F_G)_x/F_G#
#=>(F_G)_x=F_Gsin(theta)#
Because
#=>color(darkblue)((F_G)_x=mgsin(theta))#
Which gives us:
#color(darkblue)(F_(x" net")=F_p-mgsin(theta))#
#color(darkblue)(F_(y" net")=0#
We can now calculate the parallel and perpendicular components of the net force.
#F_(x" net")=F_p-mgsin(theta)#
#=8"N"-(5"kg")(9.81"m"//"s"^2)sin(pi/8)#
#=-10.77"N"#
#~~-11"N"#
- Note that the negative sign indicates direction. We defined up the ramp as positive, so a negative parallel component of the net force tells us that the net force horizontally is down the ramp.

