Question

An object with a mass of `6 kg` is on a plane with an incline of `pi/12`. If the object is being pushed up the plane with `6 N` of force, what is the net force on the object?

Answer 1

`sumF = 9.23` `"N"` directed down the plane

Explanation:

I'll assume the surface is frictionless, as there is no information regarding friction given.

Referring to the image below:

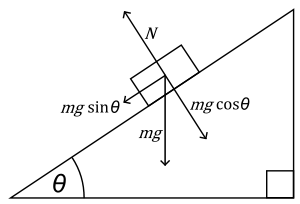
I'll call the positive `x`-axis going down the plane.

We know the normal force `n` and quantity `mgcostheta` are equal in magnitude, so we need not resolve the vertical direction.

Since the surface is (supposedly) frictionless, the only forces being applied are

• gravitation force, equal to `mgsintheta` (directed down the incline)

• applied force, equal to `6` `"N"` (directed up the incline)

We need to find the quantity `mgsintheta` by knowing

• `m = 6` `"kg"`

• `g = 9.81` `"m/s"^2`

• `theta = pi/12`

Therefore,

`mgsintheta = (6color(white)(l)"kg")(9.81color(white)(l)"m/s"^2)sin(pi/12) = 15.2` `"N"`

The net horizontal force `sumF_x` is given by

`sumF_x = mgsintheta - F_"applied" = 15.2` `"N"` `-6` `"N"`

`= color(red)(9.23` `color(red)("N"`

directed down the plane