An object with a mass of #8 kg# is hanging from an axle with a radius of #27 cm#. If the wheel attached to the axle has a radius of #18 cm#, how much work would it take to turn the wheel a length equal to the circumference of the axle?
1 Answer
Jan 28, 2016
Explanation:
Here's the picture as I see it:
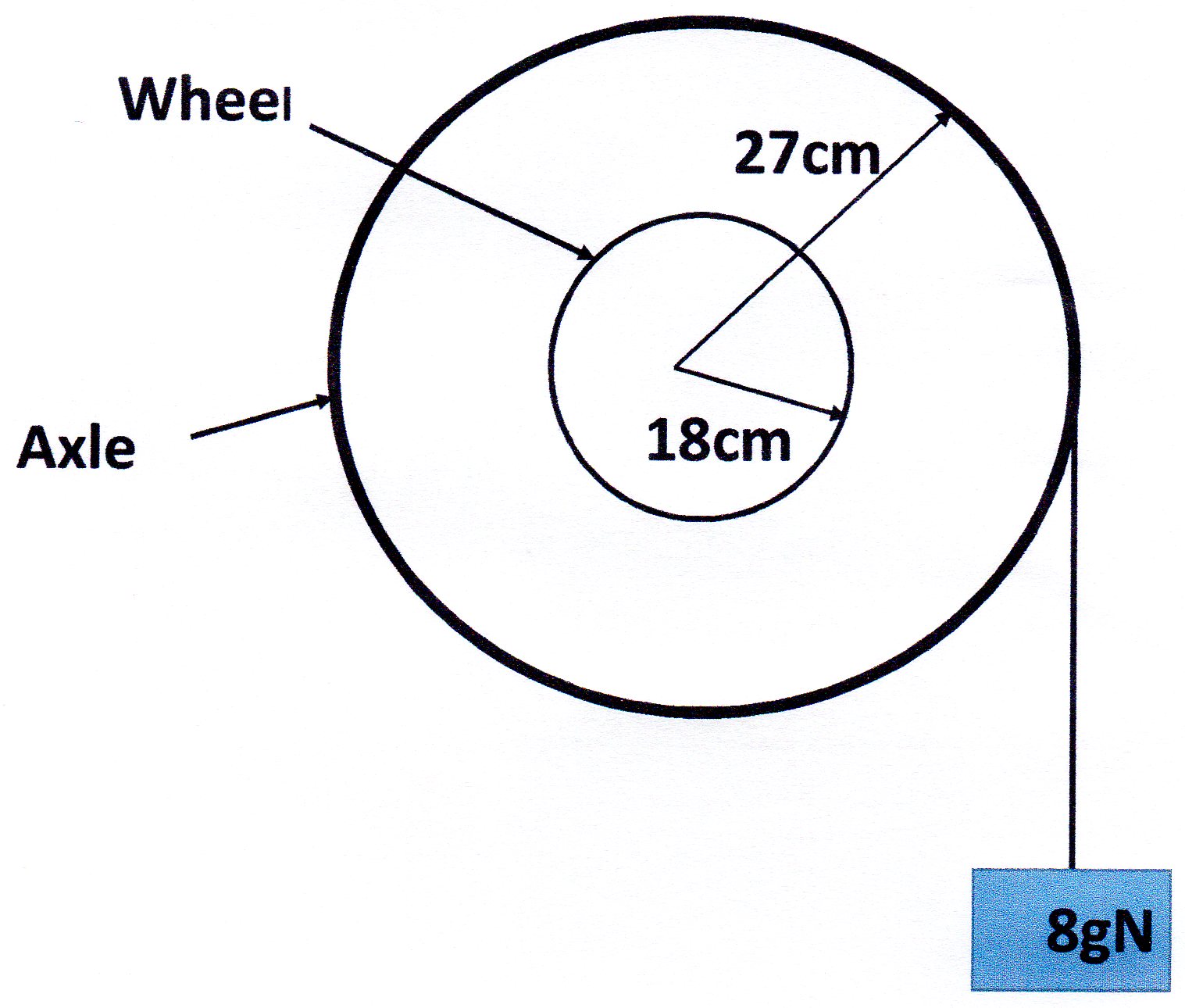
The circumference of the axle is given by:
The circumference of the wheel is given by:
If the wheel turns the circumference of the axle then it must turn through a distance of
How many turns
The no. of turns the axle completes must be the same so the total distance the axle rotates is:
The work done in lifting the 8kg mass is given by:

