An object with a mass of #9 kg# is acted on by two forces. The first is #F_1= < -7 N , 1 N># and the second is #F_2 = < 6 N, -3 N>#. What is the objects rate and direction of acceleration?

Question

1438 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-07-06T19:07:20

#a=sqrt5/9" "m/s^2#
#"Please look at the animation for direction of acceleration"#

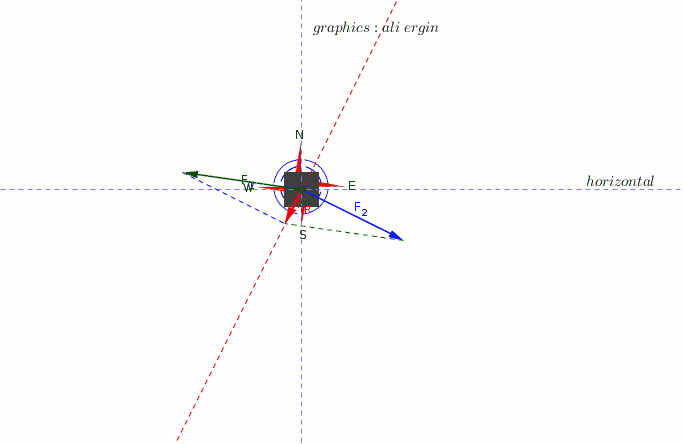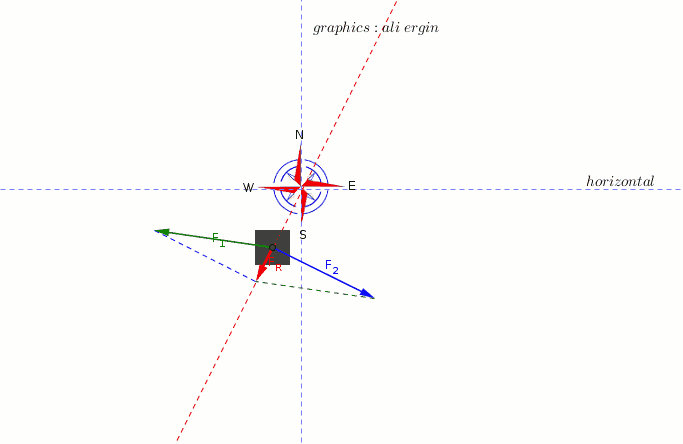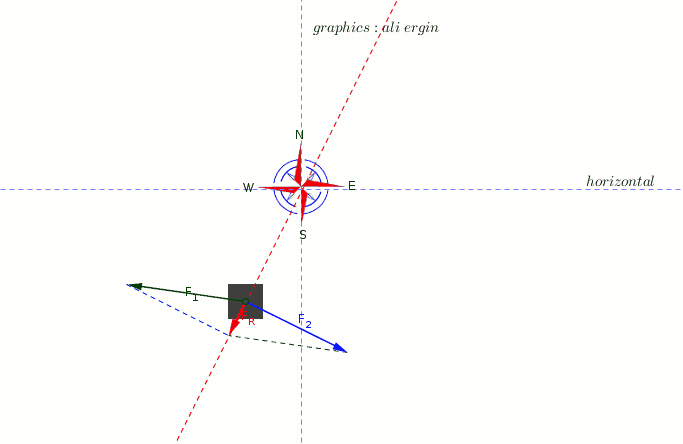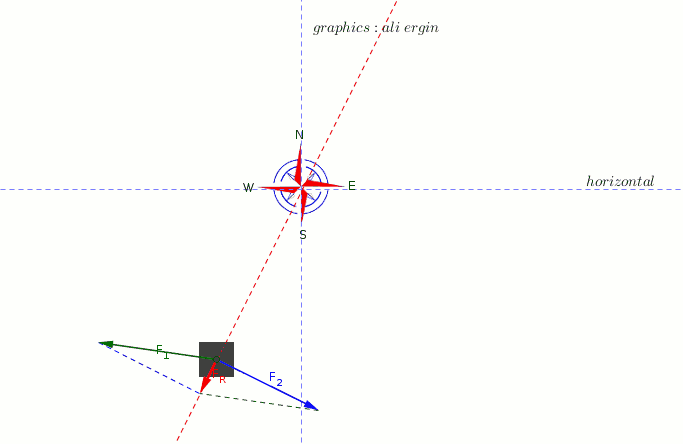
enter image source here

#"There are two force acting on body in different directions"#
#"First ,we have to find the vectorial sum of the two forces."#

#F_1= < -7,1 >" ; "F_2= <6,-3>#

#vec F_1= -7i+j" ; "vec F_2=6i-3j#

#vec F_R:"represents the vectorial sum of "vec F_1" and "vec F_2#

#vec F_R=(-7+6)i+(1-3)j#

#vec F_R=-i-2j#

#"now,we need to find the magnitude of "vec F_R#

#F_"net"=sqrt((-1)^2+(-2)^2)=sqrt(1+4)=sqrt5" "N#

#"We have to use the Newton's second law of motion :"#

#a:"represents the acceleration of object"#
#m:"represents the mass of object"#

#a=F_"net"/m#

#a=sqrt5/9" "m/s^2#

#"direction of acceleration is being shown in animation above."#