An oblique circular cylinder has height #5# and volume #45pi#. What is the radius of the circular base?

2 Answers
Nam D.
Jun 5, 2018

#3#

Explanation:

The volume of a cylinder is given by:

#V=pir^2h#

where:

  • #r# is the radius of the cylinder

  • #h# is the cylinder's height

Here, we get:

#45pi=pir^2*5#

#r^2=(45pi)/(5pi)#

#=9#

#:.r=sqrt9=3 \ (because r>0)#

Somebody N.
Jun 5, 2018

#color(blue)("radius"=3)#

Explanation:

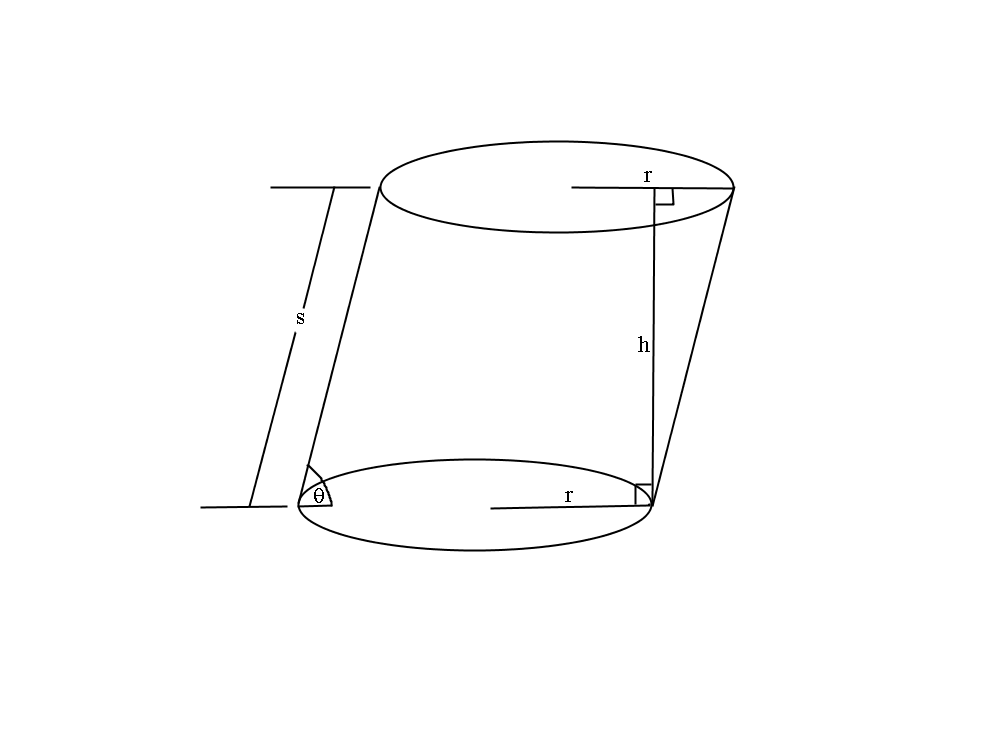
enter image source here

From the diagram, it would appear that the volume of a oblique cylinder is different from that of a right cylinder of a given height. It looks as though the actual height would be #bbs# and to find this we would need the slope length and the angle #theta# made between this side and the horizontal.

This is not the case. If we are given the radius and the perpendicular height, the volume will be the same as a right cylinder of the same height and radius. This is easier to see if we look at the volume as a series of discs.

From the two stacks we can see that the height remains the same and the volume of each disc also remains the same.

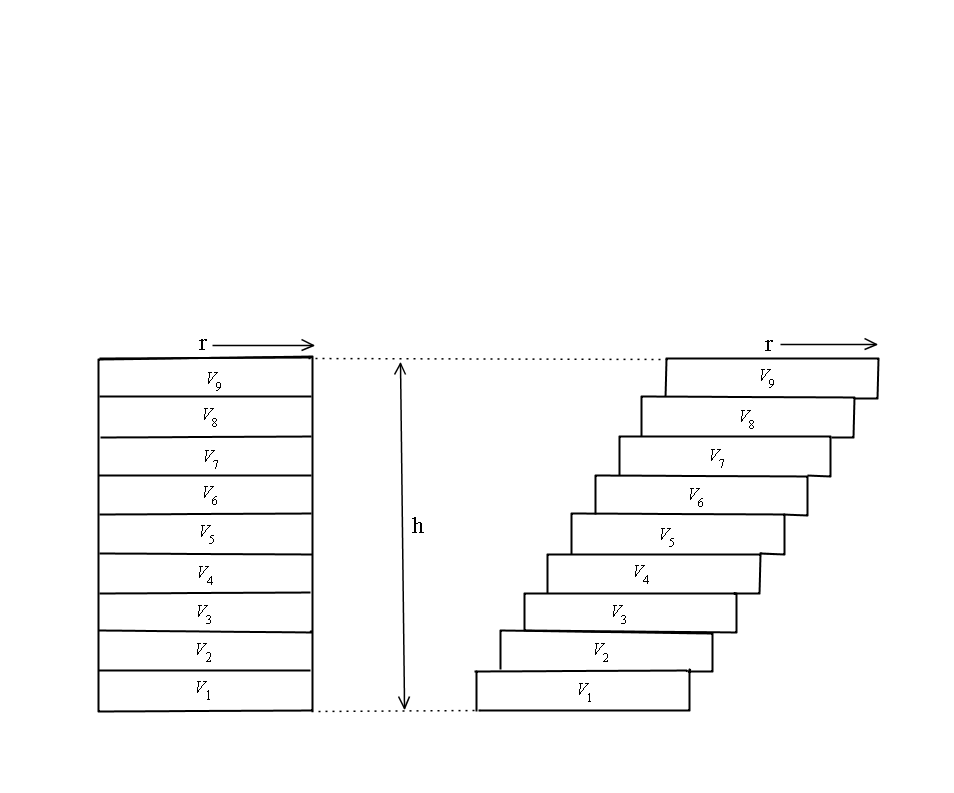
enter image source here

To solve this particular problem, we just need to look at it as a right cylinder.

The volume of a cylinder is given as:

#V="area of base"xx"height"#

#V=pir^2h#

We are given:

#h=5#

#V=45pi#

#pir^2(5)=45pi#

#r^2=(45pi)/(5pi)=9#

#r=sqrt(9)=+-3#

Negative radius not valid for this problem.

#r=3#

Related questions
Impact of this question
5244 views around the world
You can reuse this answer
Creative Commons License