Question

An open pipe has a length of 0.75 m. What would be the length of a closed organ pipe whose third harmonic(n=3) is the same as the fundamental frequency of the open pipe?

Answer 1

`3.4"m"`

Explanation:

For an open pipe the 1st harmonic looks like this:

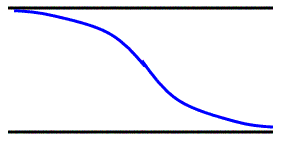
This refers to half a wavelength so:

`L_1=lambda/2`

`lambda=2L_1`

Since `v=flambda`:

`f=v/lambda=(v)/(2L_1)` `" "` `color(red)((1))`

For the closed pipe the 3rd harmonic looks like this:

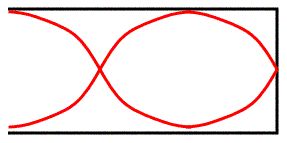
In this case:

`L_2=3/4lambda`

`lambda=(4L_2)/(3)`

So `v=f.(4L_2)/(3)`

So `f=(3v)/(4L_2)` `" "` `color(red)((2))`

These frequencies are equal so putting `color(red)((1))` equal to `color(red)((2))rArr`

`(v)/(2L_1)=(3v)/(4L_2)`

`(3)/(4L_2)=(1)/(2L_1)`

`L_2=(6L_1)/(4)`

`L_2=(3xx6xx0.75)/(4)`

`L_2=3.4"m"`