AND gate is formed by using two? 1)OR 2)NAND 3)NOT 4)NOR
2 Answers
Euhhh...
As far as I am aware...
None of the above.
Explanation:
The simplest Boolean "gate" is the identity:
Simplest: what comes in, goes out....
So simple, that it actually doesn't change anything and usually is forgotten/ignored. Compare it to a simple strip of copperwire...
The other basic gates:
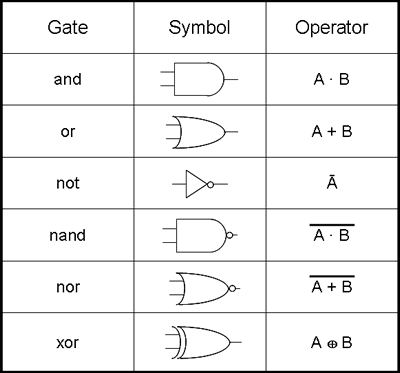
The Equals (Identity), NOT , AND, OR and XOR (Exclusive OR) are the basic, elementary gates/operators in Boolean Algebra.
So you can't really construct an AND -gate from any other ones.....
AND gate is formed by using two NAND gates.
Explanation:
NAND and NOR gates are called "Universal" gates as any kind of logic gate can be obtained by using combinations of these.
To get an AND gate we can use two NAND gates.
If A and B are the input to the first NAND gate, we will get output as
Let this be denoted by
Now give
Now the output of second NAND gate will be :
Note: AND logic can also be obtained by using 3 NOR gates. But as the question says about a specific number two , we need to use NAND gates.


