Another Circle Theorem?
1 Answer
Proof detailed below
Explanation:
I've taken your diagram throughout (thank you!)
We're going to give some names to parts of your diagram:
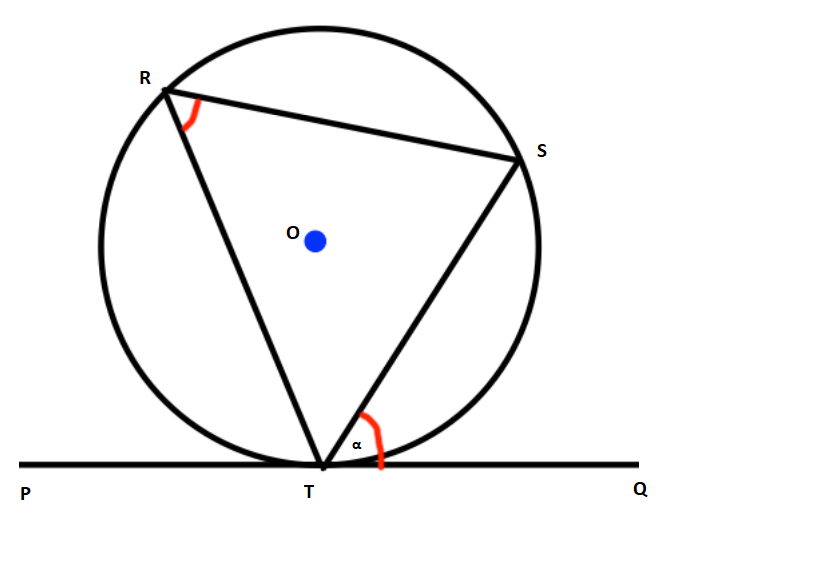
Let
We will construct two radii between
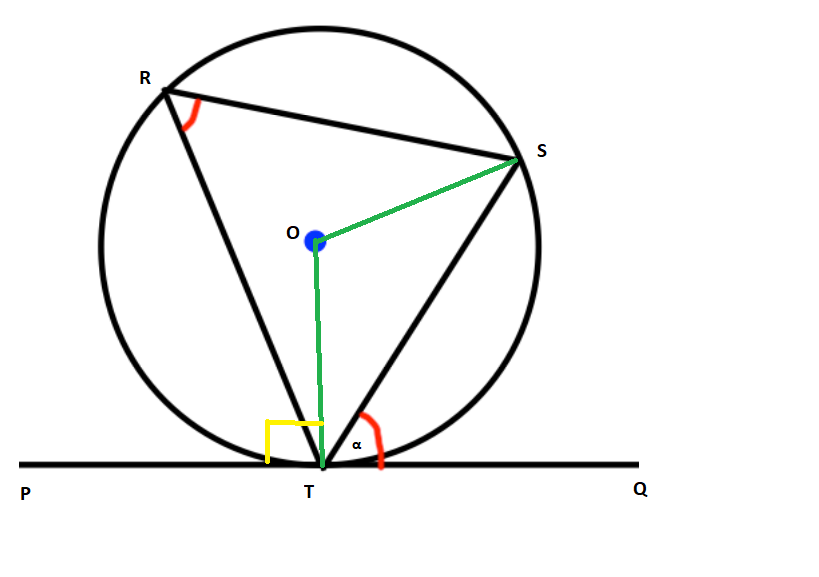
Since the angle between a tangent and a radius is a right angle,
Since OT and OS are both radii:
Since there are 180 degrees in a triangle;
Final diagram to make the last step clear:
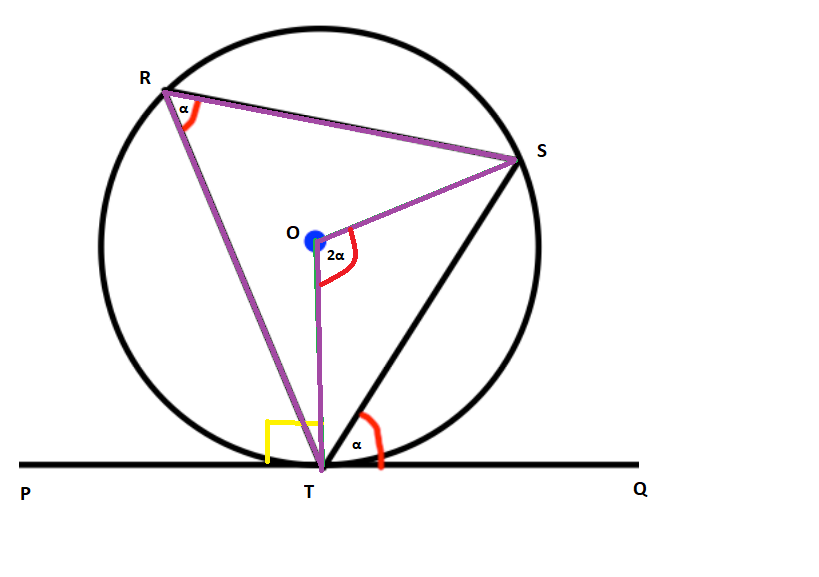
I have used purple lines to make this last bit clear. We will use another circle theorem:
The angle at the centre is twice that at the circumference
the angle between a tangent and a chord at the point of contact is equal to the angle in the alternate segment
