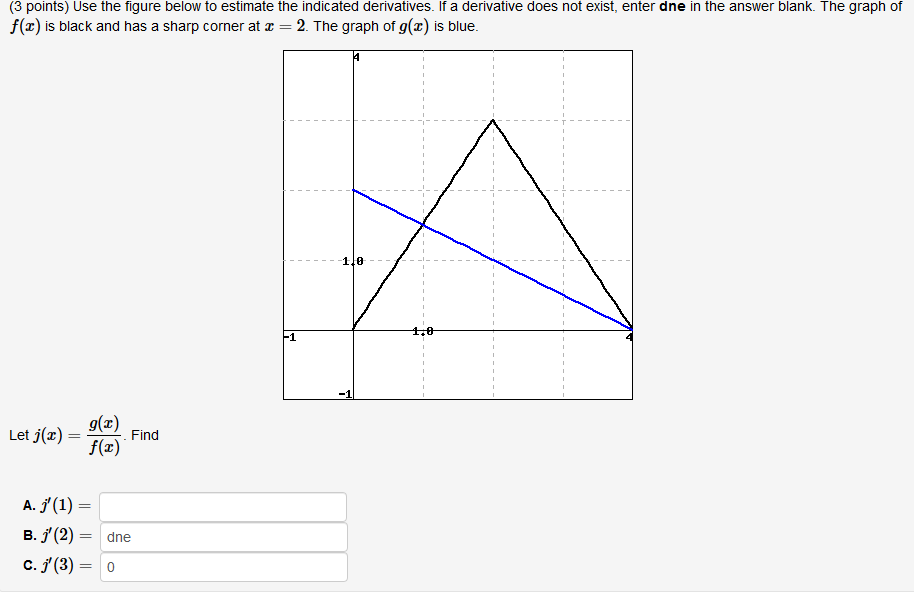
Another graph involving differentiation. This time I got j'(2) and j'(3) right, but I need help finding j'(1). Can someone help please?
1 Answer
Explanation:
This question is implicitly attempting to test you on the quotient rule.
We're given that
This is just applying the quotient rule formula.
Now, we're being asked to find
We can draw this relationship since f(x) and g(x) intersect at x = 1.
Note that since both f(x) and g(x) are linear functions, we can simply use the slope formula to find their derivatives.
Now, we plug all this into the formula:
If you need some additional help/practice on using the quotient rule, I'd encourage you to take a look at some of my videos on the subject:
Hope that helps :)

