Answer the following questions: Please refer to the questions in the image: Thank you?
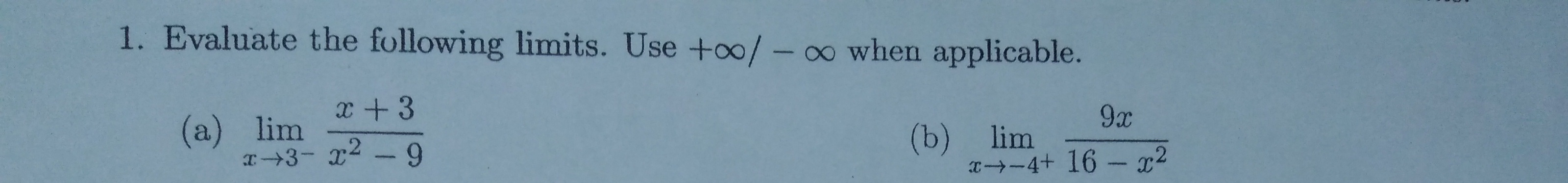
1 Answer
May 23, 2018
a)
b)
Explanation:
i will solve question 1
a)
take a number from left of 3 like 2.9
now offset it in the limit
if the sign of the limit equal
b)
take a number from right of -4 like -4.1
offset it in the limit
we will get

