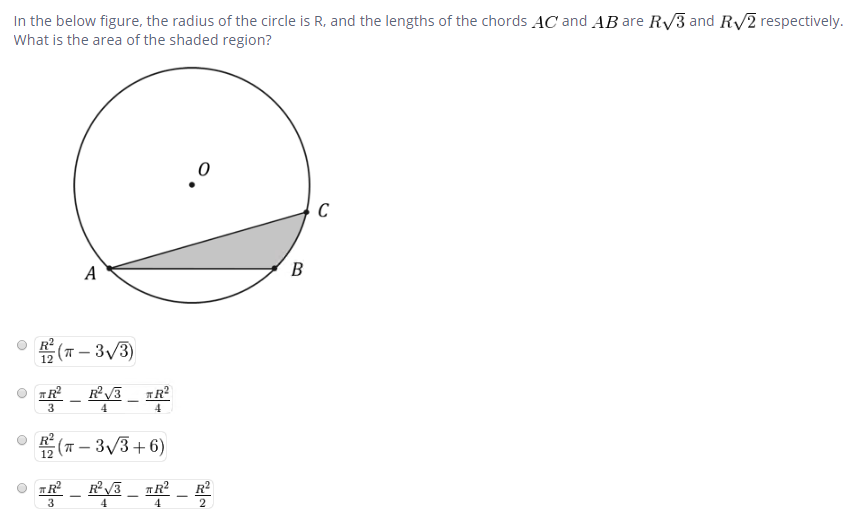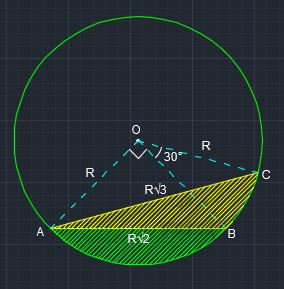
As OA=OB=R, and AB=Rsqrt2,
=> angleAOB=90^@
Use Law of cosines to find angleAOC,
cosangleAOC=(R^2+R^2-(sqrt3R)^2)/(2R^2)
=> cosangleAOC=-(R^2)/(2R^2)=-1/2
=> angleAOC=cos^-1(-1/2)=120^@
Yellow area = area of sector OAC - green area - area DeltaOAC
Area of sector OAC = piR^2(120)/360=color(red)((piR^2)/3)
Green area =area of sector OAB - area DeltaOAB
= color(red)((piR^2)/4-R^2/2)
Area DeltaOAC=1/2R^2sin120=color(red)((sqrt3R^2)/4)
Hence, yellow area
=(piR^2)/3-(R^2sqrt3)/4-(piR^2)/4+R^2/2
=R^2(pi/3-sqrt3/4-pi/4+1/2)
=R^2(pi/12-sqrt3/4+1/2)
=R^2/12(pi-3sqrt3+6)