Are there polynomial functions whose graphs have: 11 points of inflection, but no max or min ?
Are there polynomial functions whose graphs have:
1001 points of inflection, but no max or min ?
Are there polynomial functions whose graphs have:
1001 points of inflection, but no max or min ?
1 Answer
See below.
Explanation:
You can build a polynomial with as many inflexion points as needed using the truncated series expansion for
For instance, an example for
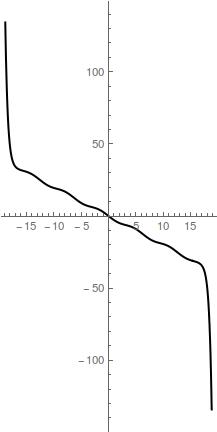
The next plot shows
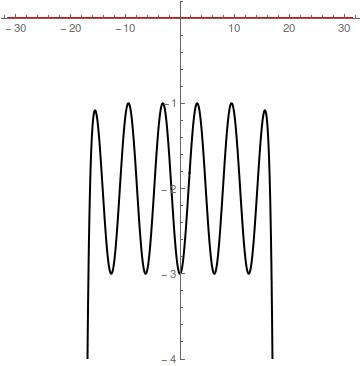
And finally the plot for
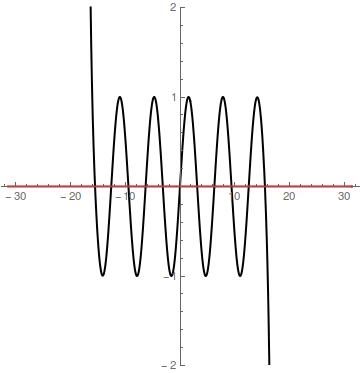
NOTE
Depending on

