Question

Area between curves?

How would you find the area between the following curves :

`x = y^4`
`y= sqrt(2-x)`
`y=0`

I know you differentiate with respect to y rather than x. I'm having trouble determining the bounds though.

Answer 1

`A_"tot" = 22/15 ~= 1.467`

Explanation:

To find the area between these curves we need to integrate them along the same axis. To begin with, the area between any curve and `y=0` is just the integral of the curve between the bounds. Next we must find the bounds.

To begin with we see that the first curve, `x=y^4` cannot have any negative values for `x`, so we can re-write it as

`y=\root(4)(x)` for `x >=0`

Then we see that for the next function to have a positive number under the square root, `2-x >= 0` or:

`y = sqrt(2-x)` for `x <=2`

Therefore the bounds for the integration must be `x_1 = 0` and `x_2 = 2`. The following graph shows the shape of the curves:

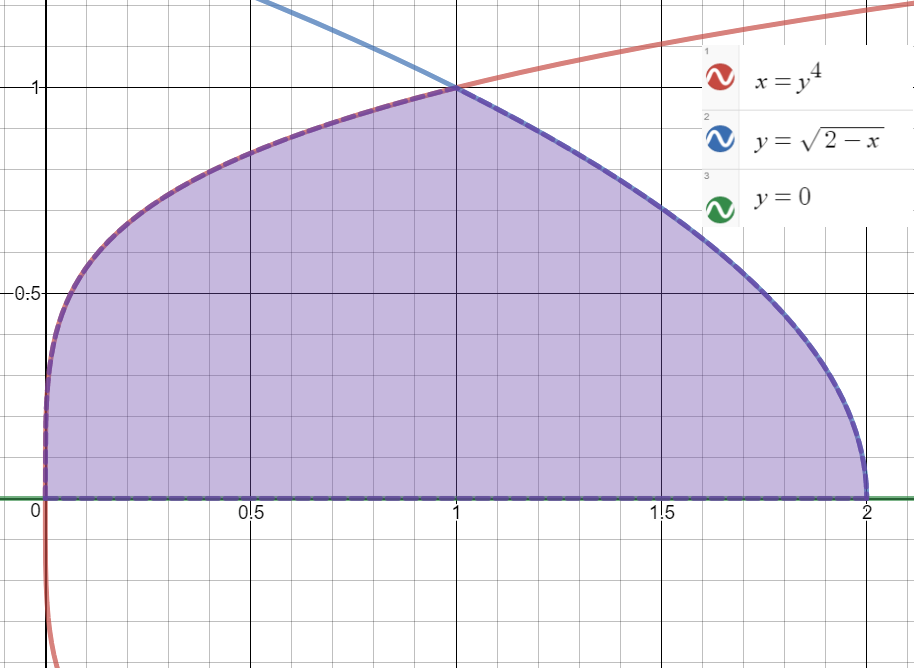
We can confirm that the two curves cross at `x=1`:

`\root(4)(1) = 1` and `sqrt(2-1) = 1`

So we can break the area up into two segments

`A_1 = \int_0^1 \root(4)(x)dx = [4/5 x^(5/4)]_0^1 = 4/5`

`A_2 = \int_1^2 sqrt(2-x) dx = [-2/3 (2 - x)^(3/2)]_1^2 = 2/3`

The total area is the sum of these two:

`A_"tot" = A_1+A_2 = 4/5+2/3 = (12+10)/15 = 22/15 ~= 1.467`