As a man walks away from a 12 foot lamppost, the tip of his shadow moves twice as fast as he does. What is the man's height?
1 Answer
Jun 10, 2018
Explanation:
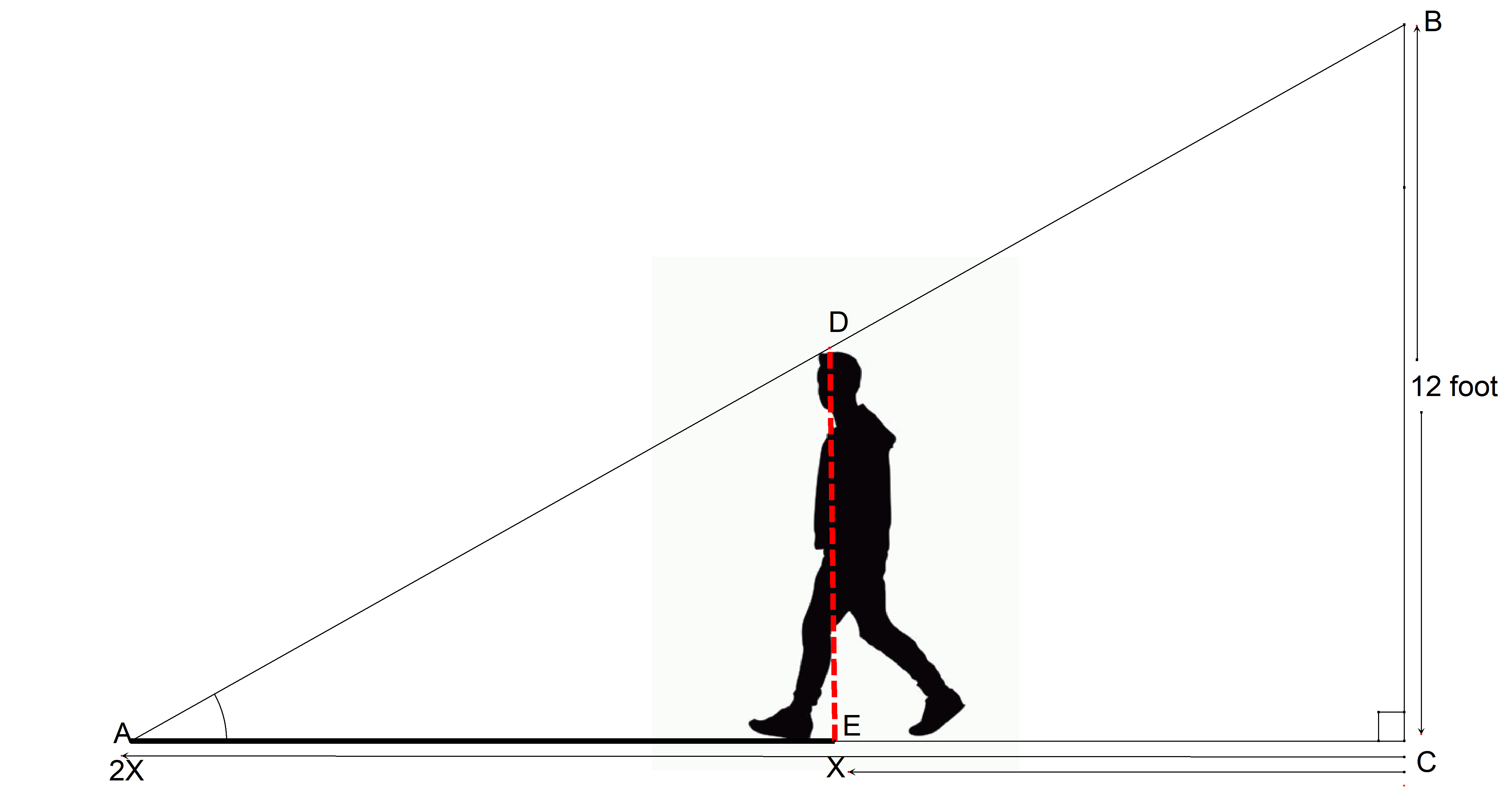
The phrase shadow moves twice as fast as he does dosen't make a lot of sense. The shadow will move at the same rate as the man. I'm guessing this really means the shadow is twice the distance from the lamp post as the man at any given time.
From the diagram:
Let the distance of the shadow from lamp be
Let the distance of the man from the lamp be
Let height of man be
Therefore:
The man is 6 foot tall.

