Question

As a man walks away from a 12-foot lamppost, the tip of his shadow moves twice as fast as he does. What is the man's height?

Answer 1

`6` feet

Explanation:

Please excuse the slightly crude diagram...

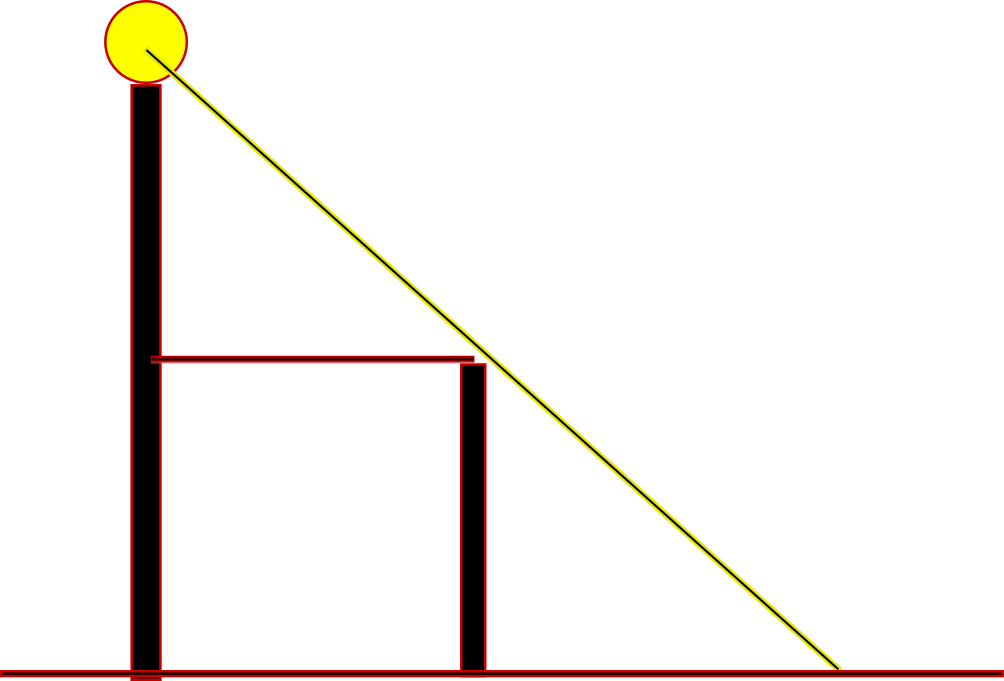
If this represents an instant of time, where the man has proceeded some distance `d` from the base of the lamp, then the base of the large triangle is `2d`, i.e. twice the base of the upper small triangle.

Since the triangles are similar, the height of the large triangle is also twice the height of the smaller triangle.

Answer 2

Calling

`x =` shadow's tip distance from lamppost.
`y =` man's distance from lamppost.
`H =` lamppost height.
`h =` man's height.

we have

`H/h = x/(x-y) rArr y = ((H-h)/H) x`

and then

`dy/dt = ((H-h)/H) dx/dt` and

`dx/dt = 2 dy/dt` and then

`((H-h)/H) =1/2 rArr h = H/2`