Assume the random variable X is normally distributed with mean μ = 50 and standard deviation σ = 7. What is the probability P (X > 42)?
1 Answer
Feb 28, 2017
# P(X>42) = 0.1271 #
Explanation:
We must standardise the Random Variable
# Z=(X-mu)/sigma #
And we will use Normal Distribution Tables of the function:
# Phi(z) = P(Z le z) #
And so we get:
# P(X>42) = P( Z > (42-50)/7 ) #
# " " = P( Z > -8/7 ) #
# " " = P( Z > -1.1429 ) #
If we look at this graphically it is the shaded part of this Standardised Normal Distribution:
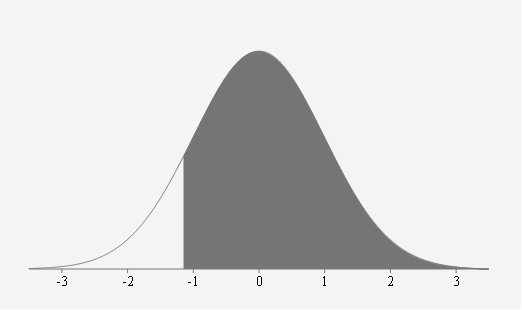
By symmetry of the Standardised Normal Distribution it is the same as this shaded part
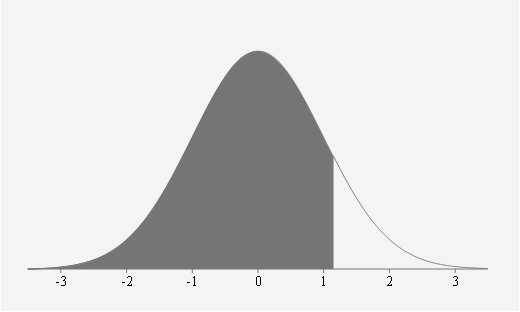
So;
# P(X>42) = P( Z > -1.1429 ) #
# " " = 1- P( Z < 1.1429 ) #
# " " = 1-Phi(1.1429 ) #
# " " = 1-0.8729 \ \ \ \ \ # (from tables)
# " " = 0.1271 #

